Recomandări pentru rezolvarea problemelor netradiționale pentru calcularea circuitelor electrice DC

Introducere

Rezolvarea problemelor este o parte integrantă a predării fizicii, deoarece în procesul de rezolvare a problemelor se formează și se îmbogățesc conceptele fizice, se dezvoltă gândirea fizică a elevilor și se îmbunătățește abilitățile lor în aplicarea cunoștințelor în practică.

În cursul rezolvării problemelor, următoarele obiective didactice pot fi stabilite și implementate cu succes:

• Ridicarea unei probleme și crearea unei situații problematice;
• Rezumarea informațiilor noi;
• Formarea deprinderilor practice;
• Testarea profunzimii și forței cunoștințelor;
• Consolidarea, generalizarea și repetarea materialului;
• Implementarea principiului politehnicismului;
• Dezvoltare creativitate elevilor.

Odată cu aceasta, atunci când rezolvă probleme, școlarii dezvoltă munca grea, o minte curios, ingeniozitate, independență în judecată, interes pentru învățare, voință și caracter și perseverență în atingerea obiectivelor. Pentru a atinge obiectivele de mai sus, este deosebit de convenabil să folosiți sarcini netradiționale.

§1. Sarcini pentru calcularea circuitelor electrice DC

Conform curriculum-ului școlar, este alocat foarte puțin timp pentru a lua în considerare această temă, astfel încât elevii stăpânesc mai mult sau mai puțin cu succes metode de rezolvare a problemelor de acest tip. Dar adesea aceste tipuri de probleme se găsesc în sarcinile olimpiadei, dar se bazează pe un curs școlar.

La astfel de probleme de calcul non-standard circuite electrice curentul continuu poate include sarcini ale căror circuite:

2) simetric;

3) constau din compuși amestecați complecși de elemente.

ÎN caz general orice circuit poate fi calculat folosind legile lui Kirchhoff. Cu toate acestea, aceste legi nu fac parte programa școlară. Mai mult, este corect să rezolvi sistemul din număr mare ecuațiile cu multe necunoscute nu sunt posibile pentru mulți studenți, iar această cale nu este cel mai bun mod pierde timpul. Prin urmare, trebuie să puteți utiliza metode care vă permit să găsiți rapid rezistența și capacitatea circuitelor.

§2. Metoda circuitului echivalent

Metoda circuitelor echivalente este aceea ca circuitul original trebuie prezentat sub forma unor secțiuni succesive, pe fiecare dintre acestea elementele circuitului sunt conectate fie în serie, fie în paralel. Pentru o astfel de reprezentare, diagrama trebuie simplificată. Prin simplificarea circuitului înțelegem conectarea sau deconectarea oricăror noduri de circuit, îndepărtarea sau adăugarea de rezistențe, condensatoare, asigurându-ne că noul circuit de elemente conectate în serie și paralel este echivalent cu cel original.

Un circuit echivalent este un circuit astfel încât atunci când aceleași tensiuni sunt aplicate circuitelor originale și convertite, curentul din ambele circuite va fi același în secțiunile corespunzătoare. În acest caz, toate calculele sunt efectuate cu circuitul convertit.

Pentru a desena un circuit echivalent pentru un circuit complex compus mixt rezistențele pot fi utilizate în mai multe moduri. Ne vom limita să luăm în considerare în detaliu doar unul dintre ele - metoda nodurilor echipotențiale.

Această metodă constă în căutarea punctelor cu potenţiale egale în circuite simetrice. Aceste noduri sunt conectate între ele și, dacă o secțiune a circuitului a fost conectată între aceste puncte, atunci este aruncată, deoarece datorită egalității potențialelor la capete, nu trece curent prin ea și această secțiune nu trece în niciun fel. afectează rezistența totală a circuitului.

Astfel, înlocuirea mai multor noduri cu potențial egal duce la un circuit echivalent mai simplu. Dar uneori este mai convenabil să înlocuiți o unitate

mai multe noduri cu potențiale egale, ceea ce nu încalcă conditiile electrice in rest.

Să ne uităm la exemple de rezolvare a problemelor folosind aceste metode.

Datorită simetriei ramurilor lanțului, punctele C și D sunt echipotențiale. Prin urmare, putem exclude rezistența dintre ele. Conectăm punctele echipotențiale C și D într-un singur nod. Obținem un circuit echivalent foarte simplu:

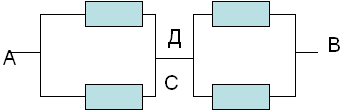
a cărui rezistență este egală cu:

RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.

Sarcina nr. 2

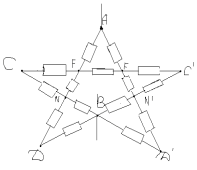
La punctele F și F` potențialele sunt egale, ceea ce înseamnă că rezistența dintre ele poate fi eliminată. Circuitul echivalent arată astfel:

Rezistențe secțiuni DNB;F`C`D`; D`, N`, B`; FCD sunt egale între ele și egale cu R1:

1/R1=1/2r+1/r=3/2r

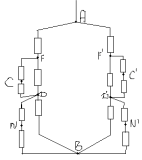
Ținând cont de acest lucru, se obține un nou circuit echivalent:

Rezistența sa și rezistența circuitului original RAB este egală cu:

1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r

Sarcina nr. 3.

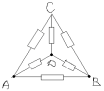
Punctele C și D au potențiale egale. Cu excepția rezistenței dintre ei. Obținem un circuit echivalent:

Rezistența necesară RAB este egală cu:

1/RAB=1/2r+1/2r+1/r=2/r

Sarcina nr. 4.

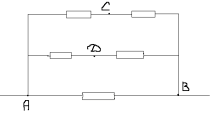
După cum se poate observa din diagramă, nodurile 1,2,3 au potențiale egale. Să le conectăm la nodul 1. Nodurile 4,5,6 au și ele potențiale egale să le conectăm la nodul 2. Obținem următorul circuit echivalent:

Rezistența din secțiunea A-1, R 1 este egală cu rezistența din secțiunea 2-B, R3 și este egală cu:

Rezistența din secțiunea 1-2 este: R2=r/6.

Acum obținem circuitul echivalent:

Rezistența totală RAB este egală cu:

RAB= R1+ R2+ R3=(5/6)*r.

Sarcina nr. 5.

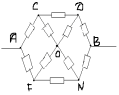
Punctele C și F sunt echivalente. Să le conectăm într-un singur nod. Atunci circuitul echivalent va arăta astfel:

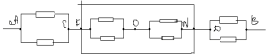
Rezistența la secțiunea AC:

Rezistenta in sectiunea FN:

Rezistență în secțiunea DB:

Rezultă un circuit echivalent:

Rezistența totală necesară este:

Problema #6

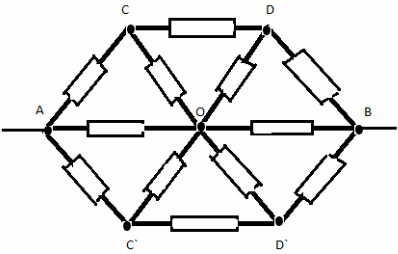
Să înlocuim nodul comun O cu trei noduri cu potențiale egale O, O 1, O 2. Obținem un sistem echivalent:

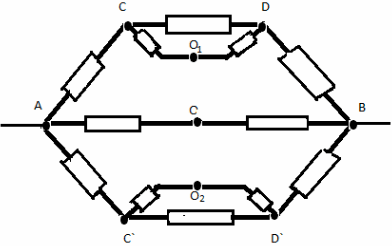
Rezistența la secțiunea ABCD:

Rezistenta in sectiunea A`B`C`D`:

Rezistență în secțiunea ACB

Obținem un circuit echivalent:

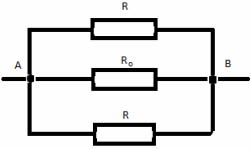
Rezistența totală necesară a circuitului R AB este egală cu:

R AB = (8/10)*r.

Sarcina nr. 7.

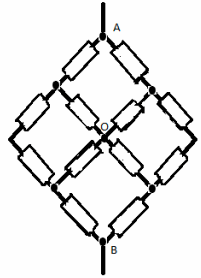
„Împărțiți” nodul O în două unghiuri echipotențiale O 1 și O 2. Acum, circuitul poate fi imaginat ca o conexiune paralelă a două circuite identice. Prin urmare, este suficient să luați în considerare unul dintre ele în detaliu:

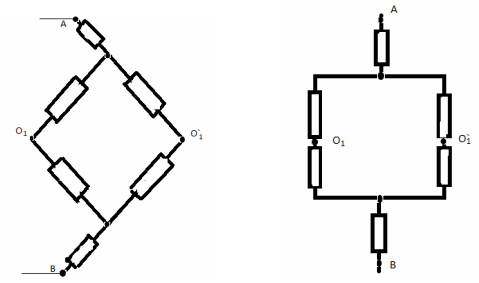
Rezistența acestui circuit R 1 este egală cu:

Apoi, rezistența întregului circuit va fi egală cu:

Sarcina nr. 8

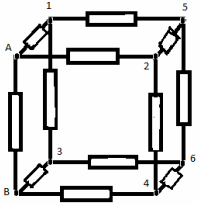
Nodurile 1 și 2 sunt echipotențiale, așa că le conectăm într-un nod I. Nodurile 3 și 4 sunt, de asemenea, echipotențiale - le conectăm într-un alt nod II. Circuitul echivalent arată astfel:

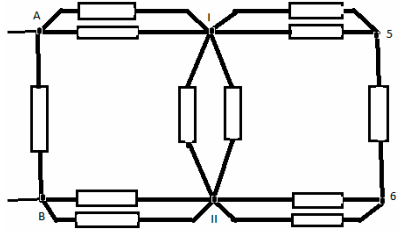
Rezistența din secțiunea A-I este egală cu rezistența din secțiunea B-II și este egală cu:

Rezistența secțiunii I-5-6-II este egală cu:

Rezistența secțiunii I-II este egală cu:

Obținem circuitul echivalent final:

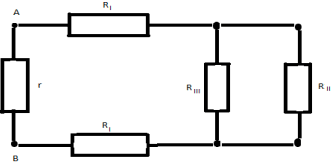
Rezistența totală necesară a circuitului este R AB = (7/12)*r.

Sarcina nr. 9

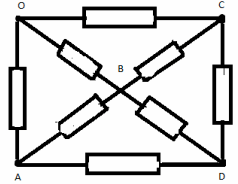
În ramura OS, înlocuim rezistența cu două rezistențe conectate în paralel de 2r. Acum nodul C poate fi împărțit în 2 noduri echipotențiale C 1 și C 2. Circuitul echivalent în acest caz arată astfel:

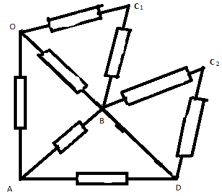
Rezistența în secțiunile OS I B și DC II B sunt aceleași și egale, deoarece este ușor de calculat 2r. Din nou desenăm circuitul echivalent corespunzător:

Rezistența din secțiunea AOB este egală cu rezistența din secțiunea ADB și este egală cu (7/4)*r. Astfel, obținem circuitul echivalent final a trei rezistențe conectate în paralel:

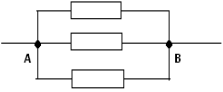
Rezistența sa totală este R AB = (7/15)*r

Sarcina nr. 10

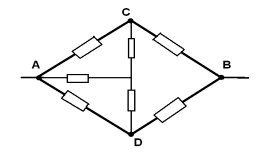
Punctele COD au potențiale egale - să le conectăm într-un singur nod O eu.Circuitul echivalent este prezentat în figură:

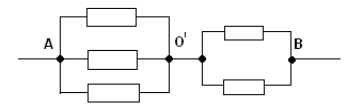
Rezistența în secțiunea A O eu egal cu . Pe site-ul O eu Rezistența este egală cu . Obținem un circuit echivalent foarte simplu:

Rezistența sa este egală cu rezistența totală dorită

Problemele nr. 11 și nr. 12 sunt rezolvate într-un mod ușor diferit față de cele anterioare. Problema nr. 11 folosește o proprietate specială a lanțurilor infinite pentru a o rezolva, iar problema nr. 12 folosește o metodă de simplificare a lanțului.

Problema nr. 11

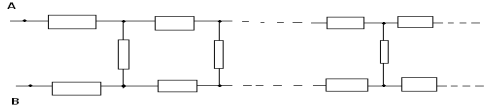
Să evidențiem o verigă care se repetă la infinit în acest lanț, în acest caz, este formată din primele trei rezistențe. Dacă aruncăm această legătură, atunci rezistența totală a circuitului infinit R nu se va schimba din această cauză, deoarece vom obține exact același circuit infinit. De asemenea, nimic nu se va schimba dacă conectăm legătura selectată înapoi la rezistența infinită R, dar ar trebui să fim atenți că o parte a legăturii și circuitul infinit cu rezistența R sunt conectate în paralel. Astfel obținem un circuit echivalent:

Se dovedește că ecuațiile

Rezolvând sistemul acestor ecuații, obținem:

§3. Instruire în rezolvarea problemelor de calcul al circuitelor electrice folosind metoda nodului echipotenţial

O problemă este o problemă care necesită ca elevul să folosească raționament logic și deducții pentru a le rezolva. Construit pe baza legilor și metodelor fizicii. Astfel, cu ajutorul sarcinilor, gândirea intenționată a elevilor este activată.

În același timp. Cunoștințele teoretice pot fi considerate dobândite doar atunci când sunt aplicate cu succes în practică. Problemele de fizică descriu probleme care se întâlnesc frecvent în viață și la locul de muncă, care pot fi rezolvate folosind legile fizicii, iar dacă elevul rezolvă cu succes problemele, atunci putem spune că cunoaște bine fizica.

Pentru ca elevii să rezolve cu succes problemele, nu este suficient să existe un set de metode și metode de rezolvare a problemelor, de asemenea, este necesar să se învețe în mod specific elevilor cum să folosească aceste metode.

Să luăm în considerare un plan pentru rezolvarea problemelor pentru calcularea circuitelor electrice DC folosind metoda nodului echipotenţial.

1. Citirea condițiilor.
2. Scurtă descriere a stării.
3. Conversia în unități SI.
4. Analiza circuitului:
1. determinați dacă circuitul este simetric;
2. stabiliți puncte de potențial egal;
3. alegeți ceea ce este mai convenabil de făcut - conectați puncte cu potențiale egale sau, dimpotrivă, împărțiți un punct în mai multe puncte cu potențiale egale;
4. desenați un circuit echivalent;
5. găsi zone cu numai secvenţial sau numai cu conexiune paralelăși calculați rezistența totală în fiecare secțiune conform legilor conexiunilor în serie și paralele;
6. desenați un circuit echivalent, înlocuind secțiunile cu rezistențele lor calculate corespunzătoare;
7. Repetați punctele 5 și 6 până când rămâne o singură rezistență, a cărei valoare va fi soluția problemei.
5. Analiza realității răspunsului.

Aflați mai multe despre analiza schemei

a) determinați dacă circuitul este simetric.

Definiţie. Un circuit este simetric dacă o jumătate din el este o imagine în oglindă a celeilalte. Mai mult, simetria nu ar trebui să fie doar geometrică, dar și valorile numerice ale rezistențelor sau condensatoarelor ar trebui să fie simetrice.

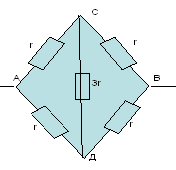
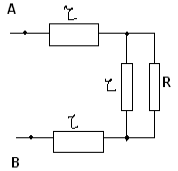
Circuitul este simetric, deoarece ramurile ASV și ADV sunt simetrice geometric și raportul de rezistență într-o secțiune AC:AD=1:1 este același ca în cealaltă secțiune SD:DV=1:1.

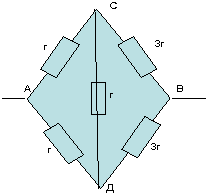
Circuitul este simetric, deoarece raportul de rezistență în secțiunea AC: AD = 1: 1 este același ca în cealaltă secțiune NE: DV = 3: 3 = 1: 1

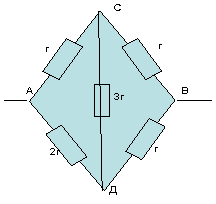
Circuitul nu este simetric, deoarece rapoartele de rezistență sunt numerice

nu simetric -1:2 și 1:1.

b) stabiliţi puncte de potenţial egal.

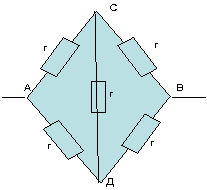
Din considerente de simetrie, concluzionăm că potențialele în puncte simetrice sunt egale. În acest caz, punctele simetrice sunt punctele C și D. Astfel, punctele C și D sunt puncte echipotențiale.

c) alegeți ce este potrivit de făcut - conectați puncte de potențial egal sau, dimpotrivă, împărțiți un punct în mai multe puncte de potențial egal.

Vedem în acest exemplu că între punctele de potențial egal C și D există o rezistență prin care curentul nu va circula. Prin urmare, putem elimina această rezistență și putem conecta punctele C și D într-un singur nod.

d) desenați un circuit echivalent.

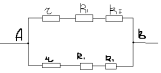
Să desenăm un circuit echivalent. În acest caz, obținem o diagramă cu punctele C și D conectate la un punct.

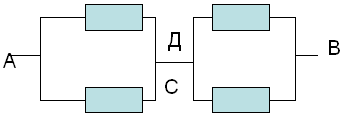
e) găsiți zone cu conexiuni numai în serie sau numai în paralel și calculați rezistența totală în fiecare astfel de zonă conform legilor conexiunilor în serie și paralele.

Din circuitul echivalent rezultat este clar că în secțiunea AC avem două rezistențe conectate în paralel. Rezistența lor totală se găsește conform legii conexiunii în paralel:

1/ Rtotal=1/R1+1/R2+1/R3+...

Astfel 1/RAC=1/r+1/r=2/r, de unde RAC= r/2.

În secțiunea NE imaginea este similară:

1/RCB= 1/r+1/r =2/r, de unde RCB=r/2.

f) desenați un circuit echivalent, înlocuind secțiunile cu rezistențele lor calculate corespunzătoare.

Desenăm un circuit echivalent, înlocuind rezistențele calculate ale secțiunilor RAC și RCB în el:

g) punctele e) și f) se repetă până când rămâne o rezistență, a cărei valoare va fi soluția problemei.

Repetăm ​​punctul d): în secțiunea AB avem două rezistențe conectate în serie. Găsim rezistența lor totală conform legii conexiunii în serie:

Rtot= R1+R2+R3+... adică RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Repetăm ​​punctul e): desenați un circuit echivalent:

Am primit un circuit cu o rezistență, a cărui valoare este egală cu rezistența circuitului original. Astfel, am primit răspunsul RAB = r.

Literatură

1. Balash. V.A. probleme de fizică și metode de rezolvare a acestora. - M: Iluminismul, 1983.
2. Lukashik V.I. Olimpiada de Fizică.- M: Educație, 2007
3. Usova A.V., Bobrov A.A. Formarea abilităților educaționale ale elevilor la lecțiile de fizică - M: Educație, 1988
4. Khatset A. Metode de calcul a circuitelor echivalente // Quantum.
5. Chertov A.G. Cartea cu probleme în fizică. – M.: Liceu, 1983
6. Ziyatdinov Sh.G., Solovyanyuk S.G. (recomandări metodologice) Birsk, 1994
7. Maron A.E., Maron E.A. Fizică. Materiale didactice. Moscova, „Bustard”, 2004

În literatură sunt descrise mai multe metode de conversie a circuitelor electrice. Aceste articole descriu, de asemenea, metode de simplificare a circuitelor care au puncte de potențial egal. Dar atunci când rezolvă astfel de probleme, autorii scriu de obicei astfel: „Din simetria ramurilor lanțului este clar că punctele ÎNŞi D au un potențial egal”, deși această apariție nu este în întregime evidentă.

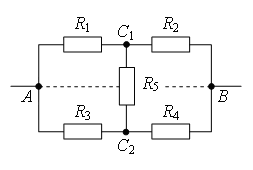
Să ne uităm la modalități de a găsi puncte cu potențial egal mai detaliat. Să ni se dea un circuit electric format din rezistențe R 1 , R 2 , …, R 8 (Fig. 1 a). Să tragem o linie dreaptă prin punctele de conectare ale circuitului AB(Fig. 1 b).

1 cale. Daca un circuit contine conductori cu aceeasi rezistenta, situati simetric fata de o anumita axa sau plan, atunci capetele acestor conductori au acelasi potential. În același timp punctele vor fi simetrice față de dreapta AB dacă rezistențele secțiunilor de circuit dintre aceste puncte și oricare dintre punctele acestei drepte sunt egale.

Folosind această caracteristică, putem concluziona că punctele CU 1 și CU 2 (Fig. 1 b) va fi simetric față de linia dreaptă AB, Dacă R 1 = R 2 (rezistența între puncte OŞi CU 1 și între punct OŞi CU 2 sunt egale) și R 5 = R 6 (rezistența între puncte ÎNŞi CU 1 și între punct ÎNŞi CU 2 sunt egale). La fel, puncte CU 3 și CU 4 va fi simetric față de o linie dreaptă AB, Dacă R 3 = R 4 și R 7 = R 8 .

O.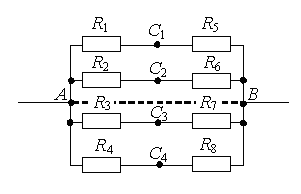

b.
Orez. 1.

Metoda 2. Punctele au același potențial dacă rapoartele de rezistență dintre aceste puncte și punctele de legătură sunt egale.

De exemplu, puncte CU 1 și CU 2 (Fig. 1 a) au acelasi potential, Dacă . La fel, puncte CU 3 și CU 4 au acelasi potential, Dacă .

Să arătăm cu exemple cum aceste metode pot fi folosite pentru a transforma circuitele electrice.

Metodă de combinare a nodurilor echipotenţiale:puncte cu potenţiale egale pot fi conectate în noduri .

Exemplul 1. Determinați rezistența circuitului electric (Fig. 2), dacă: a) R 1 = R 3 = 2R, R 2 = R 4 = R, R 5 = 3R; b) R 1 = R 4 = 2R, R 2 = 4R, R 3 = R, R 5 = 5R.

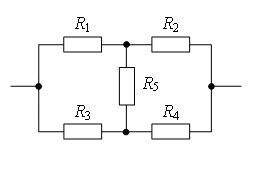
Orez. 2.

a) Dacă tragi o linie dreaptă prin punctele de legătură AB(Fig. 3 a), atunci rezistențele secțiunilor sunt egale AC 1 și AC 2 (R 1 = R 3), iar rezistențele secțiunilor sunt egale Soare 1 și Soare 2 (R 2 = R 4). Prin urmare, punctele CU 1 și CU AB si au potential egal.

Punctele cu aceleași potențiale pot fi conectate în noduri (Fig. 3, b). Rezistoare R 1 și R R 2 și R 4 – paralele, secțiuni 1/3 Şi 2/4

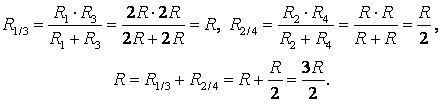
b) Dacă trasezi o linie dreaptă AB(Fig. 3 a), apoi rezistența secțiunilor AC 1 și AC 2 nu sunt egale, deci punctele CU 1 și CU 2 nu sunt simetrice față de o linie dreaptă AB. DAR puncte CU 1 și CU 2 au potentiale egale, pentru că .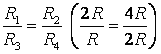

Punctele cu aceleași potențiale pot fi conectate în noduri (Fig. 3 b). Rezistoare R 1 și R 3 sunt conectate în paralel, iar rezistențele R 2 și R 4 – paralele, secțiuni 1/3 Şi 2/4 secvenţial. Prin urmare,

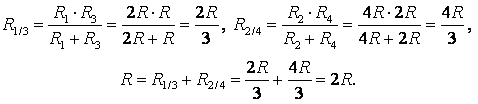
O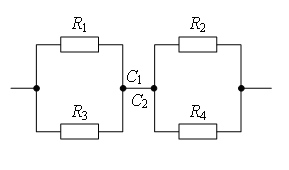

b
Orez. 3.

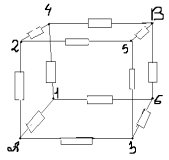
Exemplul 2 O 1 și ÎN 3 (Fig. 4). Rezistența fiecărei aripioare R 0 .

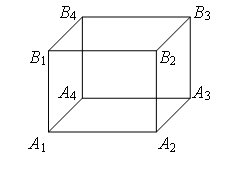
Orez. 4.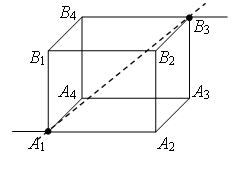

Orez. 5.

O 1 ÎN 3 (Fig. 5). Rezistențele sunt egale (lungimile nervurilor sunt egale) ale secțiunilor O 1 ÎN 1 , O 1 O 2 și O 1 O 4, iar rezistențele sunt egale (lungimile - diagonalele) secțiunilor sunt egale ÎN 3 ÎN 1 , ÎN 3 O 2 și ÎN 3 O 4. Prin urmare punctele ÎN 1 , O 2 și O O 1 ÎN 3 și au potențiale egale. Rezistențele secțiunilor sunt egale O 1 O 3 , O 1 ÎN 2 și O 1 ÎN ÎN 3 O 3 , ÎN 3 ÎN 2 și ÎN 3 ÎN 4. Prin urmare punctele O 3 , ÎN 2 și ÎN 4 sunt simetrice față de o linie dreaptă O 1 ÎN 3 și au potențiale egale.

Punctele cu aceleași potențiale pot fi conectate în noduri (Fig. 6). Trei rezistențe R 0 conectat în paralel între puncte O 1 și O 2 (ÎN 1 , O 4), șase rezistențe R O 2 (ÎN 1 , O 4) și O 3 (ÎN 2 , ÎN 4), trei rezistențe R 0 – paralelă între puncte O 3 (ÎN 2 , ÎN 4) și ÎN 3, secțiunile dintre aceste puncte sunt conectate în serie. Prin urmare,

.



Orez. 6.

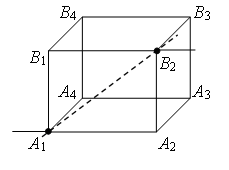
Exemplul 3. Aflați rezistența cubului de sârmă între puncte O 1 și ÎN 2 (Fig. 4). Rezistența fiecărei aripioare R 0 .

Să tragem o linie dreaptă prin punctele de legătură O 1 ÎN 2 (Fig. 7 a). Rezistențele sunt egale (lungimile nervurilor sunt egale) ale secțiunilor O 1 ÎN 1 , O 1 O 2, iar rezistențele sunt egale (lungimile nervurilor sunt egale) ale secțiunilor ÎN 2 ÎN 1 , ÎN 2 O 2. Prin urmare punctele ÎN 1 și O 2 sunt simetrice față de o dreaptă O 1 ÎN 2 și au potențiale egale. Rezistențele secțiunilor sunt egale O 1 O 3 și O 1 ÎN 4, iar rezistențele secțiunilor sunt egale ÎN 2 O 3 și ÎN 2 ÎN 4. Prin urmare, punctele O 3 și ÎN 4 O 1 simetric față de o linie dreaptă ÎN 2 și au potențiale egale.

Punctele cu aceleași potențiale pot fi conectate în noduri (Fig. 7 b). Folosind metoda recurentă, schema poate fi simplificată (Fig. 7 c sau d).

Puncte O 2 și ÎN 4 au potentiale egale, pentru că 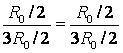. Punctele cu aceleași potențiale pot fi conectate în noduri (Fig. 7 d). Rezistoare pe șantier O 1 O 2 sunt conectate în paralel, iar rezistențele în zonă O 2 ÎN 2 – în paralel, iar aceste secțiuni sunt conectate în serie. Prin urmare,

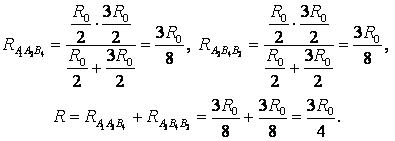
O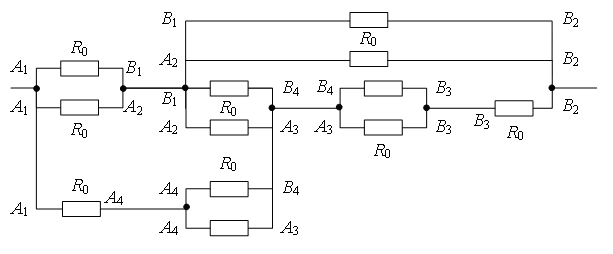



b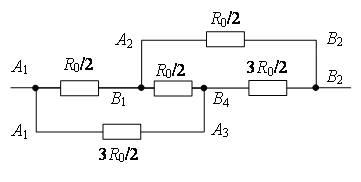

V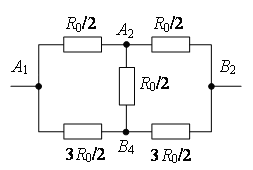

G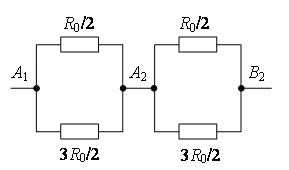

d
Orez. 7.

Dacă este posibilă unirea a două noduri echipotențiale, atunci este posibilă și tranziția inversă.

Metoda de divizare a nodurilor: un nod de circuit poate fi împărțit în două sau mai multe noduri dacă nodurile rezultate au aceleași potențiale.

O condiție prealabilă pentru aceasta este verificarea nodurilor rezultate pentru egalitatea potențialului (simetria sau proporționalitatea rezistenței).

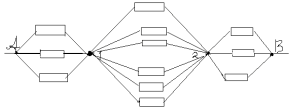
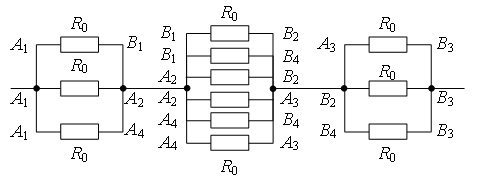
Exemplul 4. Găsiți rezistența circuitului, care este un cadru de bucăți identice de sârmă (Fig. 8) cu rezistența R 0 fiecare.

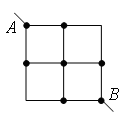
Orez. 8.

Împărțiți nodul din mijlocul cadrului în două noduri DESPRE 1 și DESPRE 2 așa cum se arată în Fig. 9 a. Acest lucru se poate face din cauza punctelor DESPRE 1 și DESPRE 2 au potențiale egale: rezistențele secțiunilor sunt egale A.O. 1 , A.O. 2, iar rezistențele secțiunilor sunt egale B.O. 1 , B.O. 2. Să redesenăm diagrama într-o formă standard (Fig. 9 b). Folosind metoda recurentă, schema poate fi simplificată (Fig. 9 c), deoarece rezistența secțiunii C 1 F 1 este egal 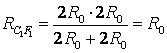, la fel. Atunci rezistența totală a circuitului este .

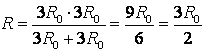Introducere

Rezolvarea problemelor este o parte integrantă a predării fizicii, deoarece în procesul de rezolvare a problemelor se formează și se îmbogățesc conceptele fizice, se dezvoltă gândirea fizică a elevilor și se îmbunătățește abilitățile lor în aplicarea cunoștințelor în practică.

În cursul rezolvării problemelor, următoarele obiective didactice pot fi stabilite și implementate cu succes:

• Ridicarea unei probleme și crearea unei situații problematice;
• Rezumarea informațiilor noi;
• Formarea deprinderilor practice;
• Testarea profunzimii și forței cunoștințelor;
• Consolidarea, generalizarea și repetarea materialului;
• Implementarea principiului politehnicismului;
• Dezvoltarea abilităților creative ale elevilor.

Odată cu aceasta, atunci când rezolvă probleme, școlarii dezvoltă munca grea, o minte curios, ingeniozitate, independență în judecată, interes pentru învățare, voință și caracter și perseverență în atingerea obiectivelor. Pentru a atinge obiectivele de mai sus, este deosebit de convenabil să folosiți sarcini netradiționale.

§1. Sarcini pentru calcularea circuitelor electrice DC

Conform curriculum-ului școlar, este alocat foarte puțin timp pentru a lua în considerare această temă, astfel încât elevii stăpânesc mai mult sau mai puțin cu succes metode de rezolvare a problemelor de acest tip. Dar adesea aceste tipuri de probleme se găsesc în sarcinile olimpiadei, dar se bazează pe un curs școlar.

Astfel de sarcini non-standard pentru calcularea circuitelor electrice DC includ sarcini ale căror diagrame sunt:

2) simetric;

3) constau din compuși amestecați complecși de elemente.

În general, orice circuit poate fi calculat folosind legile lui Kirchhoff. Cu toate acestea, aceste legi nu sunt incluse în programa școlară. În plus, nu mulți elevi pot rezolva corect un sistem de un număr mare de ecuații cu multe necunoscute, iar această cale nu este cea mai bună modalitate de a pierde timpul. Prin urmare, trebuie să puteți utiliza metode care vă permit să găsiți rapid rezistența și capacitatea circuitelor.

§2. Metoda circuitului echivalent

Metoda circuitelor echivalente este aceea ca circuitul original trebuie prezentat sub forma unor secțiuni succesive, pe fiecare dintre acestea elementele circuitului sunt conectate fie în serie, fie în paralel. Pentru o astfel de reprezentare, diagrama trebuie simplificată. Prin simplificarea circuitului înțelegem conectarea sau deconectarea oricăror noduri de circuit, îndepărtarea sau adăugarea de rezistențe, condensatoare, asigurându-ne că noul circuit de elemente conectate în serie și paralel este echivalent cu cel original.

Un circuit echivalent este un circuit astfel încât atunci când aceleași tensiuni sunt aplicate circuitelor originale și convertite, curentul din ambele circuite va fi același în secțiunile corespunzătoare. În acest caz, toate calculele sunt efectuate cu circuitul convertit.

Pentru a desena un circuit echivalent pentru un circuit cu o conexiune complexă mixtă de rezistențe, puteți utiliza mai multe tehnici. Ne vom limita să luăm în considerare în detaliu doar unul dintre ele - metoda nodurilor echipotențiale.

Această metodă constă în căutarea punctelor cu potenţiale egale în circuite simetrice. Aceste noduri sunt conectate între ele și, dacă o secțiune a circuitului a fost conectată între aceste puncte, atunci este aruncată, deoarece datorită egalității potențialelor la capete, nu trece curent prin ea și această secțiune nu trece în niciun fel. afectează rezistența totală a circuitului.

Astfel, înlocuirea mai multor noduri cu potențial egal duce la un circuit echivalent mai simplu. Dar uneori este mai convenabil să înlocuiți o unitate

mai multe noduri cu potențiale egale, ceea ce nu încalcă condițiile electrice din restul piesei.

Să ne uităm la exemple de rezolvare a problemelor folosind aceste metode.

Datorită simetriei ramurilor lanțului, punctele C și D sunt echipotențiale. Prin urmare, putem exclude rezistența dintre ele. Conectăm punctele echipotențiale C și D într-un singur nod. Obținem un circuit echivalent foarte simplu:

a cărui rezistență este egală cu:

RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.

Sarcina nr. 2

La punctele F și F` potențialele sunt egale, ceea ce înseamnă că rezistența dintre ele poate fi eliminată. Circuitul echivalent arată astfel:

Rezistențe secțiuni DNB;F`C`D`; D`, N`, B`; FCD sunt egale între ele și egale cu R1:

1/R1=1/2r+1/r=3/2r

Ținând cont de acest lucru, se obține un nou circuit echivalent:

Rezistența sa și rezistența circuitului original RAB este egală cu:

1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r

Sarcina nr. 3.

Punctele C și D au potențiale egale. Cu excepția rezistenței dintre ei. Obținem un circuit echivalent:

Rezistența necesară RAB este egală cu:

1/RAB=1/2r+1/2r+1/r=2/r

Sarcina nr. 4.

După cum se poate observa din diagramă, nodurile 1,2,3 au potențiale egale. Să le conectăm la nodul 1. Nodurile 4,5,6 au și ele potențiale egale să le conectăm la nodul 2. Obținem următorul circuit echivalent:

Rezistența din secțiunea A-1, R 1 este egală cu rezistența din secțiunea 2-B, R3 și este egală cu:

Rezistența din secțiunea 1-2 este: R2=r/6.

Acum obținem circuitul echivalent:

Rezistența totală RAB este egală cu:

RAB= R1+ R2+ R3=(5/6)*r.

Sarcina nr. 5.

Punctele C și F sunt echivalente. Să le conectăm într-un singur nod. Atunci circuitul echivalent va arăta astfel:

Rezistența la secțiunea AC:

Rezistenta in sectiunea FN:

Rezistență în secțiunea DB:

Rezultă un circuit echivalent:

Rezistența totală necesară este:

Problema #6

Să înlocuim nodul comun O cu trei noduri cu potențiale egale O, O 1, O 2. Obținem un sistem echivalent:

Rezistența la secțiunea ABCD:

Rezistenta in sectiunea A`B`C`D`:

Rezistență în secțiunea ACB

Obținem un circuit echivalent:

Rezistența totală necesară a circuitului R AB este egală cu:

R AB = (8/10)*r.

Sarcina nr. 7.

„Împărțiți” nodul O în două unghiuri echipotențiale O 1 și O 2. Acum, circuitul poate fi imaginat ca o conexiune paralelă a două circuite identice. Prin urmare, este suficient să luați în considerare unul dintre ele în detaliu:

Rezistența acestui circuit R 1 este egală cu:

Apoi, rezistența întregului circuit va fi egală cu:

Sarcina nr. 8

Nodurile 1 și 2 sunt echipotențiale, așa că le conectăm într-un nod I. Nodurile 3 și 4 sunt, de asemenea, echipotențiale - le conectăm într-un alt nod II. Circuitul echivalent arată astfel:

Rezistența din secțiunea A-I este egală cu rezistența din secțiunea B-II și este egală cu:

Rezistența secțiunii I-5-6-II este egală cu:

Rezistența secțiunii I-II este egală cu:

Obținem circuitul echivalent final:

Rezistența totală necesară a circuitului este R AB = (7/12)*r.

Sarcina nr. 9

În ramura OS, înlocuim rezistența cu două rezistențe conectate în paralel de 2r. Acum nodul C poate fi împărțit în 2 noduri echipotențiale C 1 și C 2. Circuitul echivalent în acest caz arată astfel:

Rezistența în secțiunile OS I B și DC II B sunt aceleași și egale, deoarece este ușor de calculat 2r. Din nou desenăm circuitul echivalent corespunzător:

Rezistența din secțiunea AOB este egală cu rezistența din secțiunea ADB și este egală cu (7/4)*r. Astfel, obținem circuitul echivalent final a trei rezistențe conectate în paralel:

Rezistența sa totală este R AB = (7/15)*r

Sarcina nr. 10

Punctele COD au potențiale egale - să le conectăm într-un singur nod O eu.Circuitul echivalent este prezentat în figură:

Rezistența în secțiunea A O eu egal cu . Pe site-ul O eu Rezistența este egală cu . Obținem un circuit echivalent foarte simplu:

Rezistența sa este egală cu rezistența totală dorită

Problemele nr. 11 și nr. 12 sunt rezolvate într-un mod ușor diferit față de cele anterioare. Problema nr. 11 folosește o proprietate specială a lanțurilor infinite pentru a o rezolva, iar problema nr. 12 folosește o metodă de simplificare a lanțului.

Problema nr. 11

Să evidențiem o verigă care se repetă la infinit în acest lanț, în acest caz, este formată din primele trei rezistențe. Dacă aruncăm această legătură, atunci rezistența totală a circuitului infinit R nu se va schimba din această cauză, deoarece vom obține exact același circuit infinit. De asemenea, nimic nu se va schimba dacă conectăm legătura selectată înapoi la rezistența infinită R, dar ar trebui să fim atenți că o parte a legăturii și circuitul infinit cu rezistența R sunt conectate în paralel. Astfel obținem un circuit echivalent:

Se dovedește că ecuațiile

Rezolvând sistemul acestor ecuații, obținem:

§3. Instruire în rezolvarea problemelor de calcul al circuitelor electrice folosind metoda nodului echipotenţial

O problemă este o problemă care necesită ca elevul să folosească raționament logic și deducții pentru a le rezolva. Construit pe baza legilor și metodelor fizicii. Astfel, cu ajutorul sarcinilor, gândirea intenționată a elevilor este activată.

În același timp. Cunoștințele teoretice pot fi considerate dobândite doar atunci când sunt aplicate cu succes în practică. Problemele de fizică descriu probleme care se întâlnesc frecvent în viață și la locul de muncă, care pot fi rezolvate folosind legile fizicii, iar dacă elevul rezolvă cu succes problemele, atunci putem spune că cunoaște bine fizica.

Pentru ca elevii să rezolve cu succes problemele, nu este suficient să existe un set de metode și metode de rezolvare a problemelor, de asemenea, este necesar să se învețe în mod specific elevilor cum să folosească aceste metode.

Să luăm în considerare un plan pentru rezolvarea problemelor pentru calcularea circuitelor electrice DC folosind metoda nodului echipotenţial.

1. Citirea condițiilor.
2. Scurtă descriere a stării.
3. Conversia în unități SI.
4. Analiza circuitului:
1. determinați dacă circuitul este simetric;
2. stabiliți puncte de potențial egal;
3. alegeți ceea ce este mai convenabil de făcut - conectați puncte cu potențiale egale sau, dimpotrivă, împărțiți un punct în mai multe puncte cu potențiale egale;
4. desenați un circuit echivalent;
5. găsiți zone cu conexiuni numai în serie sau numai în paralel și calculați rezistența totală în fiecare zonă conform legilor conexiunilor în serie și paralele;
6. desenați un circuit echivalent, înlocuind secțiunile cu rezistențele lor calculate corespunzătoare;
7. Repetați punctele 5 și 6 până când rămâne o singură rezistență, a cărei valoare va fi soluția problemei.
5. Analiza realității răspunsului.

Aflați mai multe despre analiza schemei

a) determinați dacă circuitul este simetric.

Definiţie. Un circuit este simetric dacă o jumătate din el este o imagine în oglindă a celeilalte. Mai mult, simetria nu ar trebui să fie doar geometrică, dar și valorile numerice ale rezistențelor sau condensatoarelor ar trebui să fie simetrice.

Circuitul este simetric, deoarece ramurile ASV și ADV sunt simetrice geometric și raportul de rezistență într-o secțiune AC:AD=1:1 este același ca în cealaltă secțiune SD:DV=1:1.

Circuitul este simetric, deoarece raportul de rezistență în secțiunea AC: AD = 1: 1 este același ca în cealaltă secțiune NE: DV = 3: 3 = 1: 1

Circuitul nu este simetric, deoarece rapoartele de rezistență sunt numerice

nu simetric -1:2 și 1:1.

b) stabiliţi puncte de potenţial egal.

Din considerente de simetrie, concluzionăm că potențialele în puncte simetrice sunt egale. În acest caz, punctele simetrice sunt punctele C și D. Astfel, punctele C și D sunt puncte echipotențiale.

c) alegeți ce este potrivit de făcut - conectați puncte de potențial egal sau, dimpotrivă, împărțiți un punct în mai multe puncte de potențial egal.

Vedem în acest exemplu că între punctele de potențial egal C și D există o rezistență prin care curentul nu va circula. Prin urmare, putem elimina această rezistență și putem conecta punctele C și D într-un singur nod.

d) desenați un circuit echivalent.

Să desenăm un circuit echivalent. În acest caz, obținem o diagramă cu punctele C și D conectate la un punct.

e) găsiți zone cu conexiuni numai în serie sau numai în paralel și calculați rezistența totală în fiecare astfel de zonă conform legilor conexiunilor în serie și paralele.

Din circuitul echivalent rezultat este clar că în secțiunea AC avem două rezistențe conectate în paralel. Rezistența lor totală se găsește conform legii conexiunii în paralel:

1/ Rtotal=1/R1+1/R2+1/R3+...

Astfel 1/RAC=1/r+1/r=2/r, de unde RAC= r/2.

În secțiunea NE imaginea este similară:

1/RCB= 1/r+1/r =2/r, de unde RCB=r/2.

f) desenați un circuit echivalent, înlocuind secțiunile cu rezistențele lor calculate corespunzătoare.

Desenăm un circuit echivalent, înlocuind rezistențele calculate ale secțiunilor RAC și RCB în el:

g) punctele e) și f) se repetă până când rămâne o rezistență, a cărei valoare va fi soluția problemei.

Repetăm ​​punctul d): în secțiunea AB avem două rezistențe conectate în serie. Găsim rezistența lor totală conform legii conexiunii în serie:

Rtot= R1+R2+R3+... adică RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Repetăm ​​punctul e): desenați un circuit echivalent:

Am primit un circuit cu o rezistență, a cărui valoare este egală cu rezistența circuitului original. Astfel, am primit răspunsul RAB = r.

Literatură

1. Balash. V.A. probleme de fizică și metode de rezolvare a acestora. - M: Iluminismul, 1983.
2. Lukashik V.I. Olimpiada de Fizică.- M: Educație, 2007
3. Usova A.V., Bobrov A.A. Formarea abilităților educaționale ale elevilor la lecțiile de fizică - M: Educație, 1988
4. Khatset A. Metode de calcul a circuitelor echivalente // Quantum.
5. Chertov A.G. Cartea cu probleme în fizică. – M.: Liceu, 1983
6. Ziyatdinov Sh.G., Solovyanyuk S.G. (recomandări metodologice) Birsk, 1994
7. Maron A.E., Maron E.A. Fizică. Materiale didactice. Moscova, „Bustard”, 2004