Препоръки за решаване на нетрадиционни задачи за изчисляване на DC електрически вериги
Въведение
Решаването на проблеми е неразделна част от обучението по физика, тъй като в процеса на решаване на задачи се формират и обогатяват физически понятия, развива се физическото мислене на учениците и се подобряват уменията им за прилагане на знанията на практика.
В хода на решаването на задачи могат да бъдат поставени и успешно реализирани следните дидактически цели:
- Предлагане на проблем и създаване на проблемна ситуация;
- Обобщаване на нова информация;
- Формиране на практически умения и способности;
- Проверка на дълбочината и силата на знанията;
- Затвърдяване, обобщаване и повторение на материала;
- Осъществяване на принципа на политехниката;
- развитие креативностстуденти.
Наред с това, при решаването на проблеми, учениците се възпитават в трудолюбие, любознателност на ума, изобретателност, независимост в преценките, интерес към ученето, воля и характер, постоянство в постигането на целта. За постигането на тези цели е особено удобно да се използват нетрадиционни задачи.
§едно. Задачи за изчисляване на електрически вериги постоянен ток
Според училищната програма се отделя много малко време за разглеждане на тази тема, така че учениците повече или по-малко успешно овладяват методите за решаване на проблеми от този тип. Но често този тип задачи се срещат в олимпиадните задачи, но те се основават на училищния курс.
Към такива нестандартни задачи за изчисление електрически веригина постоянен ток могат да се припишат задачи, чиито схеми:
2) симетричен;
3) се състоят от сложни смесени съединения от елементи.
Като цяло всяка верига може да се изчисли с помощта на законите на Кирхоф. Тези закони обаче не са училищна програма. Освен това малко ученици могат да решат правилно система от голям брой уравнения с много неизвестни и този път не е по най-добрия начингубя време. Следователно трябва да можете да използвате методи, които ви позволяват бързо да намерите съпротивлението и капацитета на веригите.
§2. Метод на еквивалентна схема
Методът на еквивалентните схеми е, че оригиналната схема трябва да бъде представена под формата на последователни секции, във всяка от които елементите на веригата са свързани последователно или паралелно. За такова представяне схемата трябва да бъде опростена. Под опростяване на веригата имаме предвид свързването или изключването на всякакви възли на веригата, премахването или добавянето на резистори, кондензатори, гарантирайки, че новата верига от последователно и паралелно свързани елементи е еквивалентна на оригиналната.
Еквивалентна верига е такава верига, че когато едно и също напрежение се приложи към оригиналната и преобразуваната верига, токът в двете вериги ще бъде еднакъв в съответните секции. В този случай всички изчисления се правят с преобразуваната схема.
Да се начертае еквивалентна схема за верига с комплекс смесена връзкарезисторите могат да се използват по няколко начина. Ще се ограничим да разгледаме подробно само един от тях - методът на еквипотенциалните възли.
Този метод се състои в това, че в симетрични вериги се намират точки с еднакви потенциали. Тези възли са свързани помежду си и ако между тези точки е включен някакъв участък от веригата, той се изхвърля, тъй като поради равенството на потенциалите в краищата токът не протича през него и този участък не влияе общото съпротивление на веригата.
По този начин замяната на няколко възела с еднакви потенциали води до по-проста еквивалентна схема. Но понякога е по-целесъобразно да се замени обратно един възел
няколко възела с еднакви потенциали, което не нарушава електрически условияв останалото.
Помислете за примери за решаване на проблеми с тези методи.
Поради симетрията на клоновете на веригата точките C и D са еквипотенциални. Следователно можем да изключим резистора между тях. Свързваме еквипотенциалните точки C и D в един възел. Получаваме много проста еквивалентна схема:
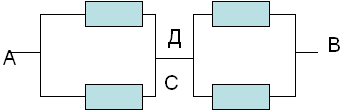
чието съпротивление е:
RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.
Задача No2
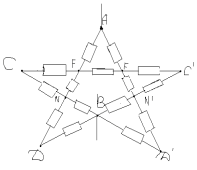
В точките F и F` потенциалите са равни, което означава, че съпротивлението между тях може да се отхвърли. Еквивалентната схема изглежда така:
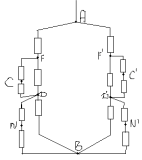
Секционни съпротивления DNB;F`C`D`; D`, N`, B`; FCD са равни помежду си и са равни на R1:
1/R1=1/2r+1/r=3/2r
Като се има предвид това, се получава нова еквивалентна схема:
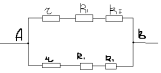
Неговото съпротивление и съпротивлението на оригиналната верига RAB е равно на:
1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r
Задача No3.
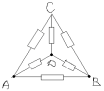
Точките C и D имат равни потенциали. Изключение прави съпротивата между тях. Получаваме еквивалентната схема:
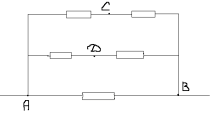
Желаното съпротивление RAB е равно на:
1/RAB=1/2r+1/2r+1/r=2/r
Задача No4.
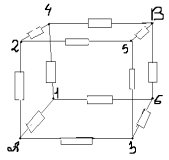
Както се вижда от диаграмата, възли 1,2,3 имат равни потенциали. Нека ги свържем към възел 1. Възлите 4,5,6 също имат равни потенциали - нека ги свържем към възел 2. Получаваме следната еквивалентна схема:
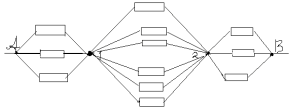
Съпротивлението в сечение A-1, R 1 е равно на съпротивлението в сечение 2-B, R3 и е равно на:
Съпротивлението в участък 1-2 е: R2=r/6.
Сега получаваме еквивалентната схема:
Общото съпротивление RAB е:
RAB \u003d R1 + R2 + R3 \u003d (5/6) * r.
Задача No5.
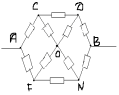
Точки C и F-еквивалент. Нека ги свържем в един възел. Тогава еквивалентната схема ще изглежда така:
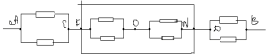
AC раздел съпротивление:
Съпротивление в раздел FN:
Съпротивление в раздел DB:
Оказва се еквивалентната схема:
Желаното общо съпротивление е равно на:
Задача №6
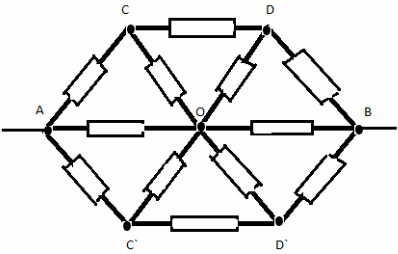
Нека заменим общия възел O с три възела с еднакви потенциали O, O 1 , O 2 . Получаваме еквивалентната система:
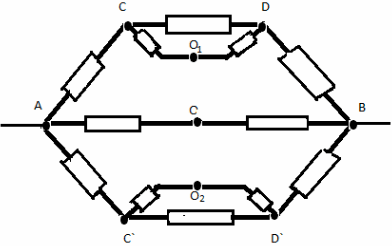
Съпротивление в участък ABCD:
Съпротивление в участък A`B`C`D`:
Съпротивление в секцията ACB
Получаваме еквивалентната схема:
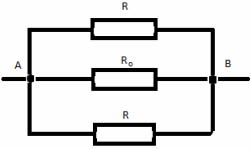
Желаното общо съпротивление на веригата R AB е:
R AB = (8/10)*r.
Задача номер 7.
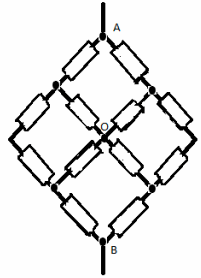
Нека “разделим” възела O на два еквипотенциални ъгъла O 1 и O 2 . Сега веригата може да бъде представена като паралелна връзка на две идентични вериги. Следователно е достатъчно да разгледаме един от тях подробно:
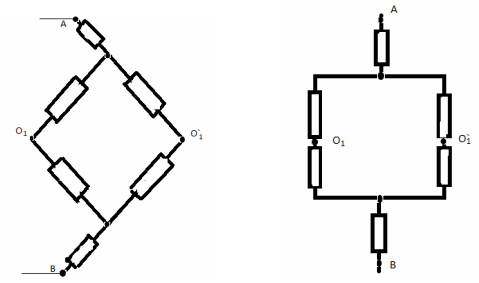
Съпротивлението на тази верига R 1 е:
Тогава съпротивлението на цялата верига ще бъде равно на:
Задача No8
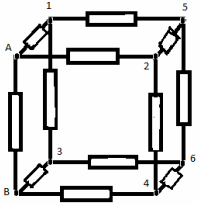
Възли 1 и 2 са еквипотенциални, така че нека ги свържем в един възел I. Възли 3 и 4 също са еквипотенциални - свързани в друг възел II. Еквивалентната схема изглежда така:
Съпротивлението в сечение A-I е равно на съпротивлението в сечение B-II и е равно на:
Съпротивлението на участък I-5-6-II е:
Съпротивлението на раздел I-II е равно на:
Получаваме крайната еквивалентна схема:
Желаното общо съпротивление на веригата R AB \u003d (7/12) * r.
Задача No9
В клона OS заместваме съпротивлението с две паралелно свързани съпротивления от 2r всяко. Сега възел C може да бъде разделен на 2 еквипотенциални възела C 1 и C 2. Еквивалентната схема в този случай изглежда така:
Съпротивленията в участъците OS I B и DC II B са еднакви и равни, тъй като е лесно да се изчисли 2r. Отново начертаваме съответната еквивалентна схема:
![]()
Съпротивлението в секцията AOB е равно на съпротивлението в секцията ADB и е равно на (7/4)*r. Така получаваме крайната еквивалентна схема на три паралелно свързани резистора:
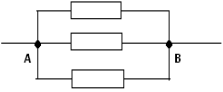
Общото му съпротивление е R AB = (7/15)*r
Задача No10
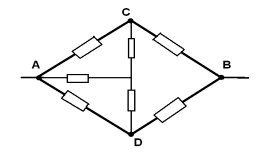
COD точките имат равни потенциали - нека ги свържем в един възел O аз.Еквивалентната схема е показана на фигурата:
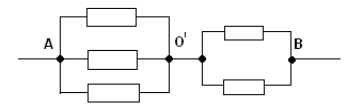
Съпротивление в раздел A O азсе равнява . На участъка О азСъпротивлението е равно на. Получаваме много проста еквивалентна схема:
![]()
НЕГОВОТО съпротивление е равно на желаното общо съпротивление
Задачи № 11 и № 12 са решени по малко по-различен начин от предишните. В задача 11 се използва специално свойство на безкрайните вериги за нейното решаване, а в задача 12 се използва метод за опростяване на веригата.
Задача номер 11
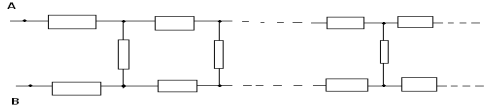
Нека отделим една безкрайно повтаряща се връзка в тази верига; в този случай тя се състои от първите три съпротивления. Ако изхвърлим тази връзка, тогава общото съпротивление на безкрайната верига R няма да се промени от това, тъй като ще се получи точно същата безкрайна верига. Освен това нищо няма да се промени, ако свържем избраната връзка обратно към безкрайното съпротивление R, но трябва да се отбележи, че част от връзката и безкрайната верига със съпротивление R са свързани паралелно. Така получаваме еквивалентната схема:
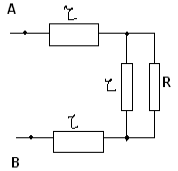
Оказва се уравненията
Решавайки системата от тези уравнения, получаваме:
§3. Научаване за решаване на задачи за изчисляване на електрически вериги по метода на еквипотенциалните възли
Задачата е проблем, за който ученикът ще се нуждае от логически разсъждения и заключения. Изграден на базата на законите и методите на физиката. Така с помощта на задачите се активизира целенасоченото мислене на учениците.
В същото време. Теоретичните знания могат да се считат за придобити само когато са успешно приложени на практика. Проблемите по физика описват проблеми, които често се срещат в живота и на работното място, които могат да бъдат решени с помощта на законите на физиката и ако ученикът успешно реши задачите, тогава можем да кажем, че познава физиката добре.
За да могат учениците успешно да решават проблеми, не е достатъчно да имате набор от методи и методи за решаване на проблеми, необходимо е също така специално да научите учениците как да използват тези методи.
Помислете за план за решаване на проблеми за изчисляване на DC електрически вериги по метода на еквипотенциалните възли.
- Условия за четене.
- Кратко изложение на условието.
- Преобразуване в SI единици.
- Анализ на веригата:
- определи дали веригата е симетрична;
- зададени точки на равен потенциал;
- изберете какво е по-целесъобразно да направите - свържете точки с равни потенциали или, обратно, разделете една точка на няколко точки с равни потенциали;
- начертайте еквивалентна схема;
- намерете сюжети само със сериал или само с паралелна връзкаи изчислете общото съпротивление във всяка секция според законите на серийното и паралелното свързване;
- начертайте еквивалентна схема, като замените секциите със съответните им проектни съпротивления;
- повторете стъпки 5 и 6, докато остане едно съпротивление, чиято стойност ще бъде решението на проблема.
- Анализ на реалността на отговора.
Научете повече за анализа на схемата
а) определете дали веригата е симетрична.
Определение. Една верига е симетрична, ако едната половина е огледален образ на другата. Освен това симетрията не трябва да бъде само геометрична, но числените стойности на съпротивленията или кондензаторите също трябва да бъдат симетрични.
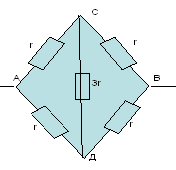
Веригата е симетрична, тъй като клоновете ASV и ADV са геометрично симетрични и съпротивлението в едната секция AS:AD=1:1 е същото като в другата секция SD:DV=1:1.
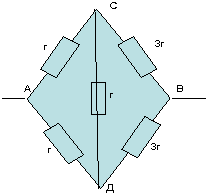
Веригата е симетрична, тъй като съотношението на съпротивленията в участъка AS:AD=1:1 е същото като в другия участък SV:DV=3:3=1:1
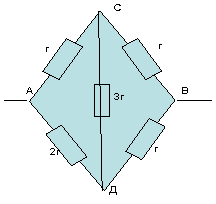
Веригата не е симетрична, тъй като съотношенията на съпротивленията са числени
не симетрични -1:2 и 1:1.
б) установете точки с равни потенциали.
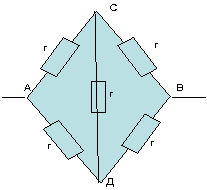
От съображения за симетрия заключаваме, че потенциалите са равни в симетрични точки. В този случай симетричните точки са точки C и D. По този начин точките C и D са еквипотенциални точки.
в) изберете какво е целесъобразно да направите - свържете точки с равни потенциали или, обратно, разделете една точка на няколко точки с равни потенциали.
Виждаме в този пример, че съпротивлението е включено между точки с равни потенциали C и D, през които няма да тече ток. Следователно можем да отхвърлим това съпротивление и да свържем точки C и D в един възел.
г) начертайте еквивалентна схема.
Начертаваме еквивалентна схема. В този случай получаваме схема с точки C и D, свързани в една точка.
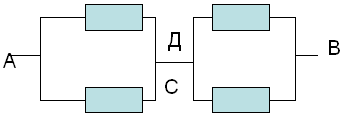
д) намерете секции само с последователна или само паралелна връзка и изчислете общото съпротивление във всяка такава секция според законите на последователната и паралелната връзка.
От получената еквивалентна схема се вижда, че в AC секцията имаме два паралелно свързани резистора. Тяхното общо съпротивление се намира съгласно закона за паралелно свързване:
1/ Rtot=1/R1+1/R2+1/R3+...
Така 1/RAC=1/r+1/r=2/r, откъдето RAC= r/2.
В секцията NE картината е подобна:
1/RCB= 1/r+1/r =2/r, откъдето RCB=r/2.
д) начертайте еквивалентна схема, като замените секциите със съответните им проектни съпротивления.
Начертаваме еквивалентна верига, като заместваме изчислените съпротивления на секциите RAC и RCB в нея:
![]()
g) точки e) и f) повтаряйте, докато остане едно съпротивление, чиято стойност ще бъде решението на задачата.
Повтаряме параграфа д): на секция AB имаме два резистора, свързани последователно. Общото им съпротивление се намира съгласно закона за серийното свързване:
Rtot= R1+R2+R3+... тоест RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повтаряме параграфа д): начертайте еквивалентна схема:

Получаваме верига с едно съпротивление, чиято стойност е равна на съпротивлението на оригиналната верига. Така получихме отговора RAB = r.
Литература
- Балаш. В.А. задачи по физика и методи за тяхното решаване. - М: Просвещение, 1983.
- Лукашик В.И. Олимпиада по физика - М: Образование, 2007 г
- Усова А.В., Бобров А.А. Формиране на образователни умения и способности на учениците в уроците по физика.- М: Образование, 1988 г.
- Khatset A. Методи за изчисляване на еквивалентни схеми // Kvant.
- Чертов А. Г. Задачна книга по физика. - М .: Висше училище, 1983
- Зиятдинов Ш.Г., Соловянюк С.Г. (насоки) Бирск, 1994
- Марон А.Е., Марон Е.А. Физика. Дидактически материали. Москва, "Дрофа", 2004 г
В литературата са описани няколко метода за преобразуване на електрически вериги. Тези статии също описват методи за опростяване на вериги с точки с еднакъв потенциал. Но когато решават такива задачи, авторите обикновено пишат така: „От симетрията на клоновете на веригата е ясно, че точките ATи димат еднакъв потенциал", въпреки че този външен вид не е съвсем очевиден.
Нека разгледаме по-подробно начините за намиране на точки със същия потенциал. Нека ни е дадена електрическа верига, състояща се от съпротивления Р 1 , Р 2 , …, Р 8 (фиг. 1а). Нека начертаем права линия през точките на свързване на веригата AB(фиг. 1b).
1 начин. Ако веригата съдържа проводници с еднакво съпротивление, разположени симетрично спрямо определена ос или равнина, тогава краищата на тези проводници имат еднакъв потенциал. При което точките ще бъдат симетрични по отношение на правата линия AB, ако съпротивленията на участъците на веригата между дадените точки и всяка точка от тази права линия са равни.
Използвайки тази функция, можем да заключим, че точките ОТ 1 и ОТ 2 (фиг. 1 b) ще бъде симетрична спрямо правата линия AB, ако Р 1 = Р 2 (съпротивление между точка НОи ОТ 1 и между точка НОи ОТ 2 са равни) и Р 5 = Р 6 (съпротивление между точка ATи ОТ 1 и между точка ATи ОТ 2 са равни). По същия начин, точки ОТ 3 и ОТ 4 ще бъде симетрично спрямо права линия AB, ако Р 3 = Р 4 и Р 7 = Р 8 .
НО. 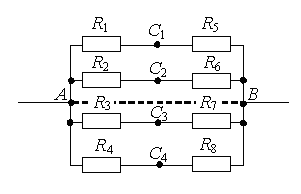
b.
Ориз. един.
2 начина. Точките имат еднакъв потенциал, ако съотношенията на съпротивленията между дадените точки и точките на свързване са равни.
Например точки ОТ 1 и ОТ 2 (фиг. 1 а) имат същия потенциал, ако . По същия начин, точки ОТ 3 и ОТ 4 имат същия потенциал, ако .
Ще покажем с примери как тези методи могат да се използват за преобразуване на електрически вериги.
Методът за комбиниране на еквипотенциални възли: точки с същите потенциалимогат да бъдат свързани на възли .
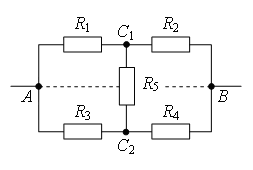
Пример 1. Определете съпротивлението на електрическата верига (фиг. 2), ако: а) Р 1 = Р 3 = 2Р, Р 2 = Р 4 = Р, Р 5 = 3Р; б) Р 1 = Р 4 = 2Р, Р 2 = 4Р, Р 3 = Р, Р 5 = 5Р.
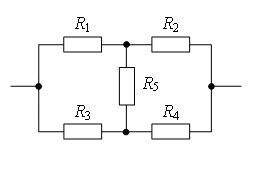
Ориз. 2.
а) Ако начертаете права линия през точките на свързване AB(фиг. 3 а), тогава съпротивленията на сеченията са равни AC 1 и AC 2 (Р 1 = Р 3) и са равни на съпротивлението на секциите слънце 1 и слънце 2 (Р 2 = Р 4). Следователно, точките ОТ 1 и ОТ ABи имат равен потенциал.
Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 3, b). Резистори Р 1 и Р Р 2 и Р 4 - паралелно, секции 1/3 и 2/4
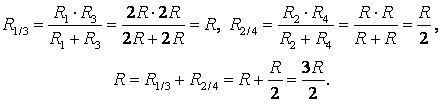
б) Ако начертаете права линия AB(фиг. 3 а), след това съпротивлението на сеченията AC 1 и AC 2 не са равни, оттам и точките ОТ 1 и ОТ 2 не са симетрични спрямо права линия AB. НО точки ОТ 1 и ОТ 2 имат равен потенциал, защото 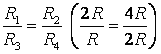 .
.
Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 3b). Резистори Р 1 и Р 3 са свързани паралелно, а резисторите Р 2 и Р 4 - паралелно, секции 1/3 и 2/4 последователно. Следователно,
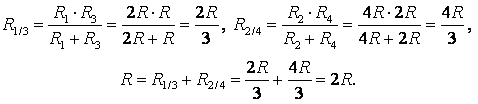
а 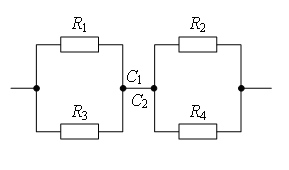
b
Ориз. 3.
Пример 2 НО 1 и AT 3 (фиг. 4). Съпротивление на всяко ребро Р 0 .
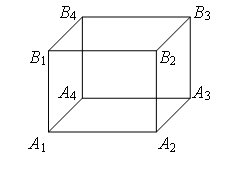
Ориз. четири. 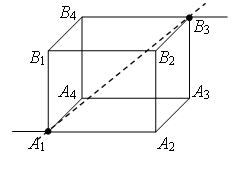
Ориз. 5.
НО 1 AT 3 (фиг. 5). Съпротивленията са равни (равни са дължините - ребрата) на сеченията НО 1 AT 1 , НО 1 НО 2 и НО 1 НО 4 , и равни съпротивления (равни дължини - диагонали) на сечения AT 3 AT 1 , AT 3 НО 2 и AT 3 НОчетири . Оттук и точките AT 1 , НО 2 и НО НО 1 AT 3 и имат равни потенциали. Са равни на съпротивлението на парцелите НО 1 НО 3 , НО 1 AT 2 и НО 1 AT AT 3 НО 3 , AT 3 AT 2 и AT 3 ATчетири . Оттук и точките НО 3 , AT 2 и AT 4 са симетрични спрямо права линия НО 1 AT 3 и имат равни потенциали.
Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 6). Три резистора Р 0 свързани паралелно между точки НО 1 и НО 2 (AT 1 , НО 4), шест резистора Р НО 2 (AT 1 , НО 4) и НО 3 (AT 2 , AT 4), три резистора Р 0 - паралел между точките НО 3 (AT 2 , AT 4) и AT 3, секциите между тези точки са свързани последователно. Следователно,
![]() .
. 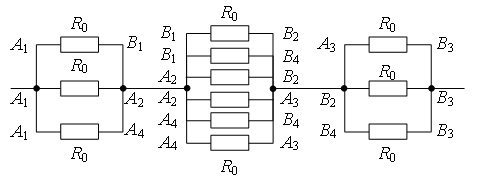
Ориз. 6.
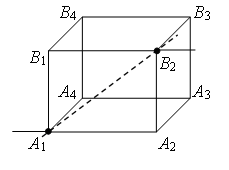
Пример 3. Намерете съпротивлението на теления куб между точките НО 1 и AT 2 (фиг. 4). Съпротивление на всяко ребро Р 0 .
Нека начертаем права линия през точките на свързване НО 1 AT 2 (фиг. 7 а). Съпротивленията са равни (равни са дължините - ребрата) на сеченията НО 1 AT 1 , НО 1 НО 2 , и сечения с равни съпротивления (равни дължини - ребра). AT 2 AT 1 , AT 2 НО 2. Оттук и точките AT 1 и НО 2 са симетрични спрямо права линия НО 1 AT 2 и имат равни потенциали. Са равни на съпротивлението на парцелите НО 1 НО 3 и НО 1 AT 4 , и са равни на съпротивлението на участъците AT 2 НО 3 и AT 2 ATчетири . Следователно, точките НО 3 и AT 4 НО 1 симетричен спрямо права линия AT 2 и имат равни потенциали.
Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 7 b). Използвайки рекурентния метод, веригата може да бъде опростена (фиг. 7 c или d).
точки НО 2 и AT 4 имат равен потенциал, защото 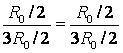 . Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 7д). Резистори на място НО 1 НО 2 са свързани паралелно, а резисторите в секцията НО 2 AT 2 - паралелно и тези секции са свързани последователно. Следователно,
. Точки с еднакви потенциали могат да бъдат свързани във възли (фиг. 7д). Резистори на място НО 1 НО 2 са свързани паралелно, а резисторите в секцията НО 2 AT 2 - паралелно и тези секции са свързани последователно. Следователно,
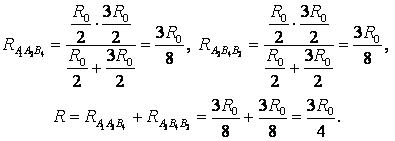
а 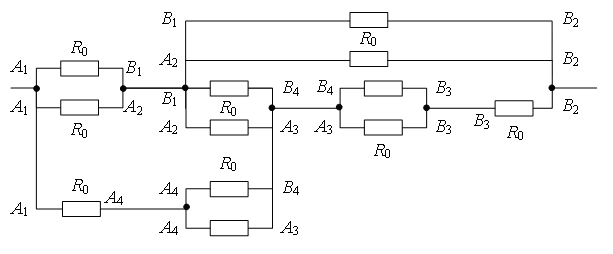
b 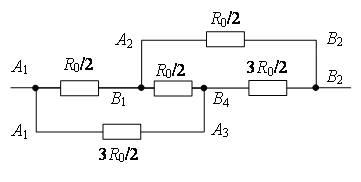
в 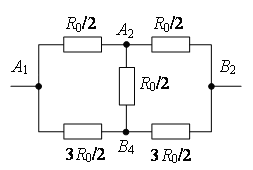
Ж 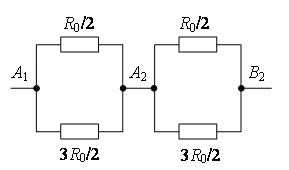
д
Ориз. 7.
Ако е възможно да се комбинират два еквипотенциални възела, тогава е възможен и обратният преход.
Метод за разделяне на възли: възел на веригата може да бъде разделен на два или повече възли, ако получените възли имат еднакви потенциали.
Предпоставка за това е да се проверят получените при разделянето възли за равенство на потенциалите (симетрия или пропорционалност на съпротивленията).
Пример 4Намерете съпротивлението на веригата, която е рамка от еднакви парчета тел (фиг. 8) със съпротивление Р 0 всеки.
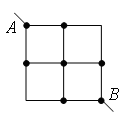
Ориз. осем.
Разделете възела в средата на рамката на два възела О 1 и О 2, както е показано на фиг. 9 а. Това може да стане, защото точките О 1 и О 2 имат равни потенциали: графики с еднакво съпротивление AO 1 , AO 2 , и са равни на съпротивлението на сеченията BO 1 , BO 2. Нека преначертаем схемата в стандартен вид (фиг. 9 b). Използвайки рекурентния метод, веригата може да бъде опростена (фиг. 9c), тъй като съпротивление на сечението ° С 1 Е 1 е равно на 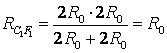 , по същия начин . Тогава общото съпротивление на веригата е
, по същия начин . Тогава общото съпротивление на веригата е 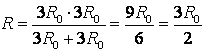 .
.
Въведение
Решаването на проблеми е неразделна част от обучението по физика, тъй като в процеса на решаване на задачи се формират и обогатяват физически понятия, развива се физическото мислене на учениците и се подобряват уменията им за прилагане на знанията на практика.
В хода на решаването на задачи могат да бъдат поставени и успешно реализирани следните дидактически цели:
- Предлагане на проблем и създаване на проблемна ситуация;
- Обобщаване на нова информация;
- Формиране на практически умения и способности;
- Проверка на дълбочината и силата на знанията;
- Затвърдяване, обобщаване и повторение на материала;
- Осъществяване на принципа на политехниката;
- Развитие на творческите способности на учениците.
Наред с това, при решаването на проблеми, учениците се възпитават в трудолюбие, любознателност на ума, изобретателност, независимост в преценките, интерес към ученето, воля и характер, постоянство в постигането на целта. За постигането на тези цели е особено удобно да се използват нетрадиционни задачи.
§едно. Задачи за изчисляване на постояннотокови електрически вериги
Според училищната програма се отделя много малко време за разглеждане на тази тема, така че учениците повече или по-малко успешно овладяват методите за решаване на проблеми от този тип. Но често този тип задачи се срещат в олимпиадните задачи, но те се основават на училищния курс.
Такива нестандартни задачи за изчисляване на DC електрически вериги включват задачи, чиито схеми са:
2) симетричен;
3) се състоят от сложни смесени съединения от елементи.
Като цяло всяка верига може да се изчисли с помощта на законите на Кирхоф. Тези закони обаче не са включени в училищната програма. Освен това малко ученици могат да решат правилно система от голям брой уравнения с много неизвестни и този начин не е най-добрият начин за губене на време. Следователно трябва да можете да използвате методи, които ви позволяват бързо да намерите съпротивлението и капацитета на веригите.
§2. Метод на еквивалентна схема
Методът на еквивалентните схеми е, че оригиналната схема трябва да бъде представена под формата на последователни секции, във всяка от които елементите на веригата са свързани последователно или паралелно. За такова представяне схемата трябва да бъде опростена. Под опростяване на веригата имаме предвид свързването или изключването на всякакви възли на веригата, премахването или добавянето на резистори, кондензатори, гарантирайки, че новата верига от последователно и паралелно свързани елементи е еквивалентна на оригиналната.
Еквивалентна верига е такава верига, че когато едно и също напрежение се приложи към оригиналната и преобразуваната верига, токът в двете вериги ще бъде еднакъв в съответните секции. В този случай всички изчисления се правят с преобразуваната схема.
Могат да се използват няколко трика, за да се начертае еквивалентна схема за верига със сложна смесена резисторна връзка. Ще се ограничим да разгледаме подробно само един от тях - методът на еквипотенциалните възли.
Този метод се състои в това, че в симетрични вериги се намират точки с еднакви потенциали. Тези възли са свързани помежду си и ако между тези точки е включен някакъв участък от веригата, той се изхвърля, тъй като поради равенството на потенциалите в краищата токът не протича през него и този участък не влияе общото съпротивление на веригата.
По този начин замяната на няколко възела с еднакви потенциали води до по-проста еквивалентна схема. Но понякога е по-целесъобразно да се замени обратно един възел
няколко възела с еднакви потенциали, което не нарушава електрическите условия в останалите.
Помислете за примери за решаване на проблеми с тези методи.
Поради симетрията на клоновете на веригата точките C и D са еквипотенциални. Следователно можем да изключим резистора между тях. Свързваме еквипотенциалните точки C и D в един възел. Получаваме много проста еквивалентна схема:
чието съпротивление е:
RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.
Задача No2
В точките F и F` потенциалите са равни, което означава, че съпротивлението между тях може да се отхвърли. Еквивалентната схема изглежда така:
Секционни съпротивления DNB;F`C`D`; D`, N`, B`; FCD са равни помежду си и са равни на R1:
1/R1=1/2r+1/r=3/2r
Като се има предвид това, се получава нова еквивалентна схема:
Неговото съпротивление и съпротивлението на оригиналната верига RAB е равно на:
1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r
Задача No3.
Точките C и D имат равни потенциали. Изключение прави съпротивата между тях. Получаваме еквивалентната схема:
Желаното съпротивление RAB е равно на:
1/RAB=1/2r+1/2r+1/r=2/r
Задача No4.
Както се вижда от диаграмата, възли 1,2,3 имат равни потенциали. Нека ги свържем към възел 1. Възлите 4,5,6 също имат равни потенциали - нека ги свържем към възел 2. Получаваме следната еквивалентна схема:
Съпротивлението в сечение A-1, R 1 е равно на съпротивлението в сечение 2-B, R3 и е равно на:
Съпротивлението в участък 1-2 е: R2=r/6.
Сега получаваме еквивалентната схема:
Общото съпротивление RAB е:
RAB \u003d R1 + R2 + R3 \u003d (5/6) * r.
Задача No5.
Точки C и F-еквивалент. Нека ги свържем в един възел. Тогава еквивалентната схема ще изглежда така:
AC раздел съпротивление:
Съпротивление в раздел FN:
Съпротивление в раздел DB:
Оказва се еквивалентната схема:
Желаното общо съпротивление е равно на:
Задача №6
Нека заменим общия възел O с три възела с еднакви потенциали O, O 1 , O 2 . Получаваме еквивалентната система:
Съпротивление в участък ABCD:
Съпротивление в участък A`B`C`D`:
Съпротивление в секцията ACB
Получаваме еквивалентната схема:
Желаното общо съпротивление на веригата R AB е:
R AB = (8/10)*r.
Задача номер 7.
Нека “разделим” възела O на два еквипотенциални ъгъла O 1 и O 2 . Сега веригата може да бъде представена като паралелна връзка на две идентични вериги. Следователно е достатъчно да разгледаме един от тях подробно:
Съпротивлението на тази верига R 1 е:
Тогава съпротивлението на цялата верига ще бъде равно на:
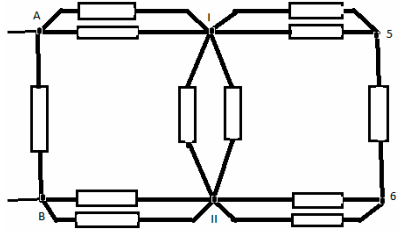
Задача No8
Възли 1 и 2 са еквипотенциални, така че нека ги свържем в един възел I. Възли 3 и 4 също са еквипотенциални - свързани в друг възел II. Еквивалентната схема изглежда така:
Съпротивлението в сечение A-I е равно на съпротивлението в сечение B-II и е равно на:
Съпротивлението на участък I-5-6-II е:
Съпротивлението на раздел I-II е равно на:
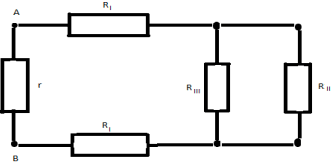
Получаваме крайната еквивалентна схема:
Желаното общо съпротивление на веригата R AB \u003d (7/12) * r.
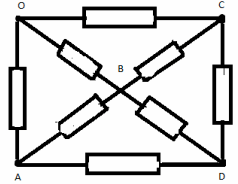
Задача No9
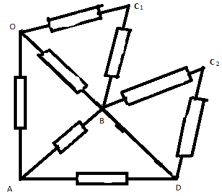
В клона OS заместваме съпротивлението с две паралелно свързани съпротивления от 2r всяко. Сега възел C може да бъде разделен на 2 еквипотенциални възела C 1 и C 2. Еквивалентната схема в този случай изглежда така:
Съпротивленията в участъците OS I B и DC II B са еднакви и равни, тъй като е лесно да се изчисли 2r. Отново начертаваме съответната еквивалентна схема:
Съпротивлението в секцията AOB е равно на съпротивлението в секцията ADB и е равно на (7/4)*r. Така получаваме крайната еквивалентна схема на три паралелно свързани резистора:
Общото му съпротивление е R AB = (7/15)*r
Задача No10
COD точките имат равни потенциали - нека ги свържем в един възел O аз.Еквивалентната схема е показана на фигурата:
Съпротивление в раздел A O азсе равнява . На участъка О азСъпротивлението е равно на. Получаваме много проста еквивалентна схема:
НЕГОВОТО съпротивление е равно на желаното общо съпротивление
Задачи № 11 и № 12 са решени по малко по-различен начин от предишните. В задача 11 се използва специално свойство на безкрайните вериги за нейното решаване, а в задача 12 се използва метод за опростяване на веригата.
Задача номер 11
Нека отделим една безкрайно повтаряща се връзка в тази верига; в този случай тя се състои от първите три съпротивления. Ако изхвърлим тази връзка, тогава общото съпротивление на безкрайната верига R няма да се промени от това, тъй като ще се получи точно същата безкрайна верига. Освен това нищо няма да се промени, ако свържем избраната връзка обратно към безкрайното съпротивление R, но трябва да се отбележи, че част от връзката и безкрайната верига със съпротивление R са свързани паралелно. Така получаваме еквивалентната схема:
Оказва се уравненията
Решавайки системата от тези уравнения, получаваме:
§3. Научаване за решаване на задачи за изчисляване на електрически вериги по метода на еквипотенциалните възли
Задачата е проблем, за който ученикът ще се нуждае от логически разсъждения и заключения. Изграден на базата на законите и методите на физиката. Така с помощта на задачите се активизира целенасоченото мислене на учениците.
В същото време. Теоретичните знания могат да се считат за придобити само когато са успешно приложени на практика. Проблемите по физика описват проблеми, които често се срещат в живота и на работното място, които могат да бъдат решени с помощта на законите на физиката и ако ученикът успешно реши задачите, тогава можем да кажем, че познава физиката добре.
За да могат учениците успешно да решават проблеми, не е достатъчно да имате набор от методи и методи за решаване на проблеми, необходимо е също така специално да научите учениците как да използват тези методи.
Помислете за план за решаване на проблеми за изчисляване на DC електрически вериги по метода на еквипотенциалните възли.
- Условия за четене.
- Кратко изложение на условието.
- Преобразуване в SI единици.
- Анализ на веригата:
- определи дали веригата е симетрична;
- зададени точки на равен потенциал;
- изберете какво е по-целесъобразно да направите - свържете точки с равни потенциали или, обратно, разделете една точка на няколко точки с равни потенциали;
- начертайте еквивалентна схема;
- намират секции само с последователно или само с паралелно свързване и изчисляват общото съпротивление във всяко сечение според законите на последователното и паралелното свързване;
- начертайте еквивалентна схема, като замените секциите със съответните им проектни съпротивления;
- повторете стъпки 5 и 6, докато остане едно съпротивление, чиято стойност ще бъде решението на проблема.
- Анализ на реалността на отговора.
Научете повече за анализа на схемата
а) определете дали веригата е симетрична.
Определение. Една верига е симетрична, ако едната половина е огледален образ на другата. Освен това симетрията не трябва да бъде само геометрична, но числените стойности на съпротивленията или кондензаторите също трябва да бъдат симетрични.
Веригата е симетрична, тъй като клоновете ASV и ADV са геометрично симетрични и съпротивлението в едната секция AS:AD=1:1 е същото като в другата секция SD:DV=1:1.
Веригата е симетрична, тъй като съотношението на съпротивленията в участъка AS:AD=1:1 е същото като в другия участък SV:DV=3:3=1:1
Веригата не е симетрична, тъй като съотношенията на съпротивленията са числени
не симетрични -1:2 и 1:1.
б) установете точки с равни потенциали.
От съображения за симетрия заключаваме, че потенциалите са равни в симетрични точки. В този случай симетричните точки са точки C и D. По този начин точките C и D са еквипотенциални точки.
в) изберете какво е целесъобразно да направите - свържете точки с равни потенциали или, обратно, разделете една точка на няколко точки с равни потенциали.
Виждаме в този пример, че съпротивлението е включено между точки с равни потенциали C и D, през които няма да тече ток. Следователно можем да отхвърлим това съпротивление и да свържем точки C и D в един възел.
г) начертайте еквивалентна схема.
Начертаваме еквивалентна схема. В този случай получаваме схема с точки C и D, свързани в една точка.
д) намерете секции само с последователна или само паралелна връзка и изчислете общото съпротивление във всяка такава секция според законите на последователната и паралелната връзка.
От получената еквивалентна схема се вижда, че в AC секцията имаме два паралелно свързани резистора. Тяхното общо съпротивление се намира съгласно закона за паралелно свързване:
1/ Rtot=1/R1+1/R2+1/R3+...
Така 1/RAC=1/r+1/r=2/r, откъдето RAC= r/2.
В секцията NE картината е подобна:
1/RCB= 1/r+1/r =2/r, откъдето RCB=r/2.
д) начертайте еквивалентна схема, като замените секциите със съответните им проектни съпротивления.
Начертаваме еквивалентна верига, като заместваме изчислените съпротивления на секциите RAC и RCB в нея:
g) точки e) и f) повтаряйте, докато остане едно съпротивление, чиято стойност ще бъде решението на задачата.
Повтаряме параграфа д): на секция AB имаме два резистора, свързани последователно. Общото им съпротивление се намира съгласно закона за серийното свързване:
Rtot= R1+R2+R3+... тоест RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повтаряме параграфа д): начертайте еквивалентна схема:
Получаваме верига с едно съпротивление, чиято стойност е равна на съпротивлението на оригиналната верига. Така получихме отговора RAB = r.
Литература
- Балаш. В.А. задачи по физика и методи за тяхното решаване. - М: Просвещение, 1983.
- Лукашик В.И. Олимпиада по физика - М: Образование, 2007 г
- Усова А.В., Бобров А.А. Формиране на образователни умения и способности на учениците в уроците по физика.- М: Образование, 1988 г.
- Khatset A. Методи за изчисляване на еквивалентни схеми // Kvant.
- Чертов А. Г. Задачна книга по физика. - М .: Висше училище, 1983
- Зиятдинов Ш.Г., Соловянюк С.Г. (насоки) Бирск, 1994
- Марон А.Е., Марон Е.А. Физика. Дидактически материали. Москва, "Дрофа", 2004 г
