Recommandations pour résoudre des problèmes non traditionnels pour le calcul de circuits électriques à courant continu

Introduction

La résolution de problèmes fait partie intégrante de l'enseignement de la physique, car dans le processus de résolution de problèmes, la formation et l'enrichissement des concepts physiques ont lieu, la pensée physique des élèves se développe et leurs compétences d'application des connaissances dans la pratique s'améliorent.

Au cours de la résolution de problèmes, les objectifs didactiques suivants peuvent être définis et mis en œuvre avec succès :

• Proposer un problème et créer une situation problématique ;
• Résumer les nouvelles informations ;
• Formation de compétences et d'aptitudes pratiques;
• Vérifier la profondeur et la force des connaissances;
• Consolidation, généralisation et répétition du matériel;
• Mise en œuvre du principe des polytechniques ;
• Développement la créativitéétudiants.

Parallèlement à cela, lors de la résolution de problèmes, les écoliers acquièrent de l'assiduité, de la curiosité d'esprit, de l'ingéniosité, de l'indépendance dans les jugements, de l'intérêt pour l'apprentissage, de la volonté et du caractère, de la persévérance dans la réalisation de l'objectif. Pour atteindre ces objectifs, il est particulièrement pratique d'utiliser des tâches non traditionnelles.

§une. Tâches pour le calcul des circuits électriques courant continu

Selon le programme scolaire, très peu de temps est alloué à l'examen de ce sujet, de sorte que les élèves maîtrisent plus ou moins bien les méthodes de résolution de problèmes de ce type. Mais souvent ces types de tâches se retrouvent dans les tâches Olympiade, mais elles sont basées sur le cursus scolaire.

À de telles tâches de calcul non standard circuits électriques courant continu peut se voir attribuer des tâches dont les schémas:

2) symétrique ;

3) consistent en des composés mixtes complexes d'éléments.

En général, tout circuit peut être calculé en utilisant les lois de Kirchhoff. Cependant, ces lois ne sont pas programme scolaire. De plus, peu d'élèves peuvent résoudre correctement un système d'un grand nombre d'équations avec de nombreuses inconnues, et ce chemin n'est pas le meilleur moyen perdre du temps. Par conséquent, vous devez pouvoir utiliser des méthodes permettant de trouver rapidement la résistance et la capacité des circuits.

§2. Méthode du circuit équivalent

La méthode des circuits équivalents est que le circuit d'origine doit se présenter sous forme de tronçons série, sur chacun desquels les éléments du circuit sont connectés soit en série, soit en parallèle. Pour une telle représentation, le schéma doit être simplifié. Sous la simplification du circuit, nous entendons la connexion ou la déconnexion de tout nœud du circuit, la suppression ou l'ajout de résistances, de condensateurs, en veillant à ce que le nouveau circuit d'éléments connectés en série et en parallèle soit équivalent à celui d'origine.

Un circuit équivalent est un circuit tel que lorsque la même tension est appliquée aux circuits d'origine et convertis, le courant dans les deux circuits sera le même dans les sections correspondantes. Dans ce cas, tous les calculs sont effectués avec le schéma converti.

Pour dessiner un circuit équivalent pour un circuit avec un complexe connexion mixte Les résistances peuvent être utilisées de plusieurs manières. Nous nous limiterons à n'en considérer en détail qu'un seul - la méthode des nœuds équipotentiels.

Cette méthode réside dans le fait que des points de potentiels égaux se trouvent dans des circuits symétriques. Ces nœuds sont connectés les uns aux autres, et si une section du circuit était incluse entre ces points, elle est alors rejetée, car en raison de l'égalité des potentiels aux extrémités, le courant ne le traverse pas et cette section n'affecte pas la résistance totale du circuit.

Ainsi, le remplacement de plusieurs nœuds de potentiels égaux conduit à un circuit équivalent plus simple. Mais parfois, il est plus opportun de remplacer à l'envers un nœud

plusieurs nœuds avec des potentiels égaux, ce qui ne viole pas conditions électriques dans le reste.

Considérons des exemples de résolution de problèmes par ces méthodes.

Du fait de la symétrie des branches de la chaîne, les points C et D sont équipotentiels. Par conséquent, nous pouvons exclure la résistance entre eux. Nous connectons les points équipotentiels C et D en un nœud. On obtient un circuit équivalent très simple :

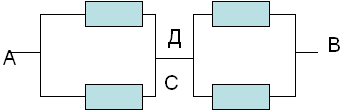
dont la résistance vaut :

RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.

Tâche n° 2

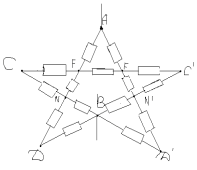
Aux points F et F', les potentiels sont égaux, ce qui signifie que la résistance entre eux peut être écartée. Le circuit équivalent ressemble à ceci :

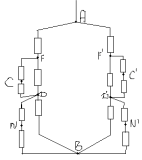
Résistances de section DNB;F`C`D`; D', N', B' ; FCD sont égaux entre eux et égaux à R1 :

1/R1=1/2r+1/r=3/2r

Dans cette optique, un nouveau circuit équivalent est obtenu :

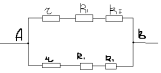
Sa résistance et la résistance du circuit d'origine RAB est égale à :

1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r

Tâche n° 3.

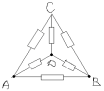
Les points C et D ont des potentiels égaux. L'exception est la résistance entre eux. On obtient le circuit équivalent :

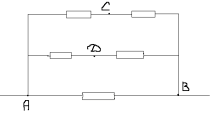
La résistance RAB souhaitée est égale à :

1/RAB=1/2r+1/2r+1/r=2/r

Tâche n° 4.

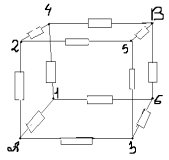
Comme on peut le voir sur le schéma, les nœuds 1, 2, 3 ont des potentiels égaux. Connectons-les au nœud 1. Les nœuds 4, 5, 6 ont également des potentiels égaux - connectons-les au nœud 2. Nous obtenons le circuit équivalent suivant :

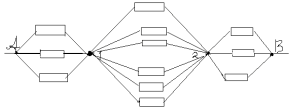
La résistance dans la section A-1, R 1 est égale à la résistance dans la section 2-B, R3 et est égale à :

La résistance dans la section 1-2 est : R2=r/6.

On obtient alors le circuit équivalent :

La résistance totale RAB est :

RAB \u003d R1 + R2 + R3 \u003d (5/6) * r.

Tâche n° 5.

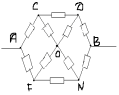
Points C et F-équivalent. Connectons-les en un seul nœud. Ensuite, le circuit équivalent ressemblera à ceci :

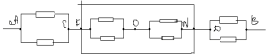
Résistance de la section CA :

Résistance dans la section FN :

Résistance dans la section DB :

Il s'avère que le circuit équivalent:

La résistance totale souhaitée est égale à :

Tâche #6

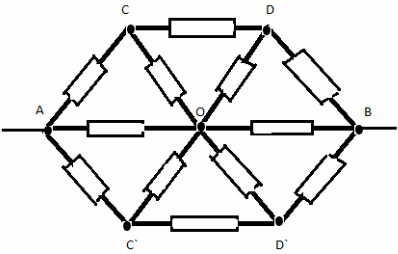
Remplaçons le noeud commun O par trois noeuds de potentiels égaux O, O 1 , O 2 . On obtient le système équivalent :

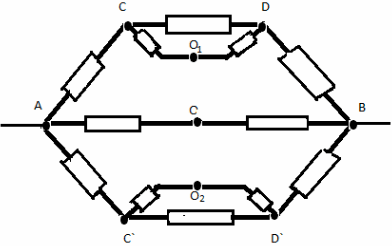
Résistance dans la section ABCD :

Résistance dans la section A`B`C`D` :

Résistance dans la section ACB

On obtient le circuit équivalent :

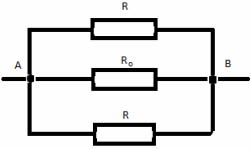
La résistance totale souhaitée du circuit R AB est :

RA AB = (8/10)*r.

Tâche numéro 7.

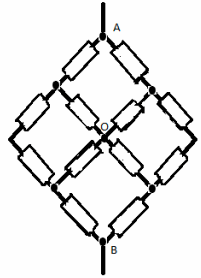
« Divisons » le nœud O en deux angles équipotentiels O 1 et O 2 . Maintenant, le circuit peut être représenté comme une connexion parallèle de deux circuits identiques. Par conséquent, il suffit d'en considérer l'un en détail:

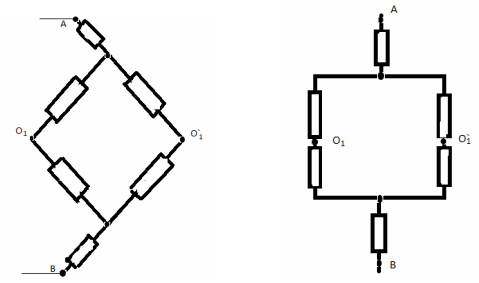
La résistance de ce circuit R 1 est :

Alors la résistance de tout le circuit sera égale à :

Tâche n° 8

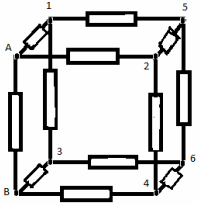
Les nœuds 1 et 2 sont équipotentiels, alors connectons-les en un nœud I. Les nœuds 3 et 4 sont également équipotentiels - connectés à un autre nœud II. Le circuit équivalent ressemble à :

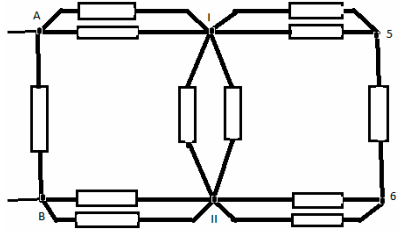
La résistance dans la section A-I est égale à la résistance dans la section B-II et est égale à :

La résistance de la section I-5-6-II est :

La résistance de la section I-II est égale à :

On obtient le circuit équivalent final :

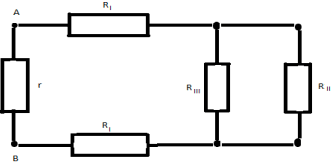
La résistance totale du circuit souhaitée R AB \u003d (7/12) * r.

Tâche n° 9

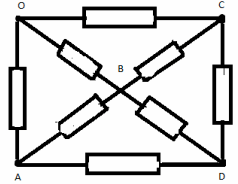
Dans la branche OS, nous remplaçons la résistance par deux résistances connectées en parallèle de 2r chacune. Maintenant le nœud C peut être divisé en 2 nœuds équipotentiels C 1 et C 2. Le circuit équivalent dans ce cas ressemble à ceci:

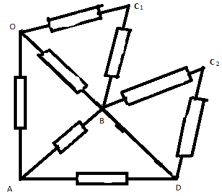
Les résistances dans les sections OS I B et DC II B sont identiques et égales, car il est facile de calculer 2r. Nous dessinons à nouveau le circuit équivalent correspondant :

La résistance dans la section AOB est égale à la résistance dans la section ADB et est égale à (7/4)*r. Ainsi, on obtient le circuit équivalent final de trois résistances connectées en parallèle :

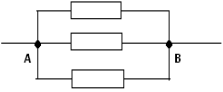
Sa résistance totale est R AB = (7/15)*r

Tâche n° 10

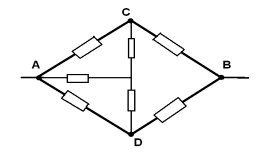
Les points COD ont des potentiels égaux - connectons-les en un seul nœud O je.Le circuit équivalent est représenté sur la figure :

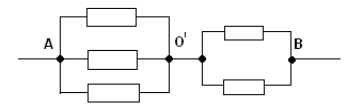
Résistance dans la section A O jeéquivaut à . Sur le tronçon O je La résistance est égale à On obtient un circuit équivalent très simple :

La résistance ITS est égale à la résistance totale souhaitée

Les problèmes n° 11 et n° 12 sont résolus d'une manière légèrement différente des précédents. Dans le problème 11, une propriété spéciale des chaînes infinies est utilisée pour le résoudre, et dans le problème 12, une méthode de simplification de chaîne est utilisée.

Tâche numéro 11

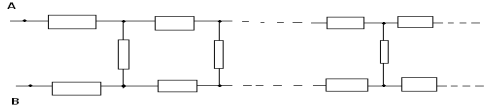
Distinguons un maillon se répétant à l'infini dans cette chaîne ; dans ce cas, il s'agit des trois premières résistances. Si nous éliminons ce lien, la résistance totale du circuit infini R ne changera pas, car exactement le même circuit infini se révélera. De plus, rien ne changera si nous reconnectons le lien sélectionné à la résistance infinie R, mais il convient de noter qu'une partie du lien et le circuit infini avec la résistance R sont connectés en parallèle. On obtient ainsi le circuit équivalent :

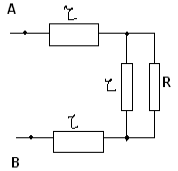
Il s'avère que les équations

En résolvant le système de ces équations, on obtient :

§3. Apprendre à résoudre des problèmes de calcul de circuits électriques par la méthode des nœuds équipotentiels

Une tâche est un problème pour lequel l'élève aura besoin de raisonnement logique et d'inférence. Construit sur la base des lois et des méthodes de la physique. Ainsi, à l'aide de tâches, la pensée délibérée des élèves est activée.

Dans le même temps. Les connaissances théoriques ne peuvent être considérées comme acquises que lorsqu'elles sont appliquées avec succès dans la pratique. Les problèmes de physique décrivent des problèmes souvent rencontrés dans la vie et au travail, qui peuvent être résolus en utilisant les lois de la physique, et si l'étudiant résout avec succès les problèmes, alors on peut dire qu'il connaît bien la physique.

Pour que les élèves réussissent à résoudre des problèmes, il ne suffit pas de disposer d'un ensemble de méthodes et de méthodes de résolution de problèmes, il est également nécessaire d'enseigner spécifiquement aux écoliers comment utiliser ces méthodes.

Considérons un plan pour résoudre les problèmes de calcul des circuits électriques à courant continu par la méthode des nœuds équipotentiels.

1. Condition de lecture.
2. Brève déclaration de l'état.
3. Convertir en unités SI.
4. Analyse des circuits :
1. déterminer si le circuit est symétrique ;
2. établir des points d'égalité de potentiel ;
3. choisissez ce qu'il est plus opportun de faire - connectez des points de potentiels égaux ou, au contraire, divisez un point en plusieurs points de potentiels égaux;
4. tracer un circuit équivalent ;
5. trouver des parcelles avec uniquement des séries ou uniquement avec connexion parallèle et calculer la résistance totale dans chaque section selon les lois de la connexion en série et en parallèle ;
6. dessiner un circuit équivalent, en remplaçant les sections par leurs résistances de conception correspondantes ;
7. répétez les étapes 5 et 6 jusqu'à ce qu'il reste une résistance dont la valeur sera la solution au problème.
5. Analyse de la réalité de la réponse.

En savoir plus sur l'analyse de schéma

a) déterminer si le circuit est symétrique.

Définition. Un circuit est symétrique si une moitié est une image miroir de l'autre. De plus, la symétrie ne doit pas seulement être géométrique, mais les valeurs numériques des résistances ou des condensateurs doivent également être symétriques.

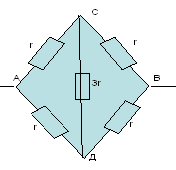
Le circuit est symétrique puisque les branches ASV et ADV sont géométriquement symétriques et que le rapport de résistance dans une section AS:AD=1:1 est le même que dans l'autre section SD:DV=1:1.

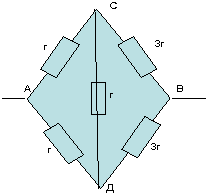
Le circuit est symétrique, car le rapport des résistances dans la section AC:BP=1:1 est le même que dans l'autre section SV:DV=3:3=1:1

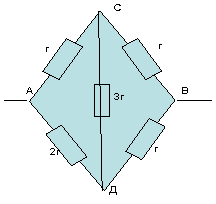
Le circuit n'est pas symétrique, puisque les rapports des résistances sont numériquement

non symétrique -1:2 et 1:1.

b) établir des points de potentiels égaux.

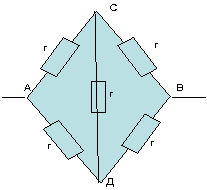
À partir de considérations de symétrie, nous concluons que les potentiels sont égaux aux points symétriques. Dans ce cas, les points symétriques sont les points C et D. Ainsi, les points C et D sont des points équipotentiels.

c) choisir ce qu'il est opportun de faire - connecter des points de potentiels égaux ou, inversement, diviser un point en plusieurs points de potentiels égaux.

Nous voyons dans cet exemple qu'une résistance est incluse entre les points de potentiels égaux C et D, à travers lesquels aucun courant ne circulera. Par conséquent, nous pouvons éliminer cette résistance et connecter les points C et D en un seul nœud.

d) tracer un circuit équivalent.

Nous dessinons un circuit équivalent. Dans ce cas, on obtient un schéma avec les points C et D connectés en un point.

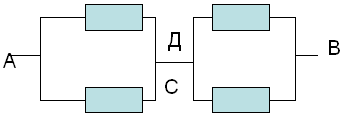
e) trouver des sections avec uniquement une connexion en série ou uniquement en parallèle et calculer la résistance totale dans chacune de ces sections selon les lois de la connexion en série et en parallèle.

D'après le circuit équivalent résultant, on peut voir que dans la section AC, nous avons deux résistances connectées en parallèle. Leur résistance totale se trouve selon la loi de mise en parallèle :

1/ Rtot=1/R1+1/R2+1/R3+…

Ainsi 1/RAC=1/r+1/r=2/r, d'où RAC= r/2.

Sur la section NE, l'image est similaire :

1/RCB= 1/r+1/r =2/r, d'où RCB=r/2.

e) dessiner un circuit équivalent, en remplaçant les sections par leurs résistances de conception correspondantes.

Nous dessinons un circuit équivalent en y substituant les résistances calculées des sections RAC et RCB :

g) points e) et f) répéter jusqu'à ce qu'il reste une résistance dont la valeur sera la solution du problème.

Nous répétons le paragraphe e): sur la section AB, nous avons deux résistances connectées en série. Leur résistance totale se trouve selon la loi de connexion en série :

Rtot= R1+R2+R3+… soit RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Nous répétons le paragraphe e): tracer un circuit équivalent :

Nous avons obtenu un circuit avec une résistance dont la valeur est égale à la résistance du circuit d'origine. Ainsi, nous avons obtenu la réponse RAB = r.

Littérature

1. Balash. VIRGINIE. problèmes de physique et méthodes pour les résoudre. - M : Lumières, 1983.
2. Lukashik V.I. Olympiade de Physique - M: Education, 2007
3. Usova A.V., Bobrov A.A. Formation des compétences pédagogiques et des capacités des étudiants en cours de physique - M: Education, 1988
4. Khatset A. Méthodes de calcul pour les circuits équivalents // Kvant.
5. Chertov A. G. Livre de tâches en physique. - M. : Ecole Supérieure, 1983
6. Ziyatdinov Sh.G., Solovyanyuk S.G. (directives) Birsk, 1994
7. Maron A.E., Maron E.A. La physique. Matériel didactique. Moscou, "Drofa", 2004

Plusieurs procédés de conversion de circuits électriques sont décrits dans la littérature. Ces articles décrivent également des méthodes de simplification des circuits avec des points d'égal potentiel. Mais lors de la résolution de tels problèmes, les auteurs écrivent généralement comme ceci: «Il ressort clairement de la symétrie des branches de la chaîne que les points À et ré ont des potentiels égaux », bien que cette apparence ne soit pas tout à fait évidente.

Examinons plus en détail les moyens de trouver des points de même potentiel. Soit donné un circuit électrique composé de résistances R 1 , R 2 , …, R 8 (Fig. 1a). Traçons une ligne droite à travers les points de connexion du circuit UN B(Fig. 1b).

1 voie. Si le circuit contient des conducteurs de même résistance, situés symétriquement autour d'un certain axe ou plan, alors les extrémités de ces conducteurs ont le même potentiel. Où les points seront symétriques par rapport à la droite AB si les résistances des sections de circuit entre les points donnés et tous les points de cette droite sont égales.

En utilisant cette caractéristique, nous pouvons conclure que les points DE 1 et DE 2 (Fig. 1 b) sera symétrique par rapport à la droite UN B, si R 1 = R 2 (résistance entre point MAIS et DE 1 et entre les points MAIS et DE 2 sont égaux) et R 5 = R 6 (résistance entre point À et DE 1 et entre les points À et DE 2 sont égaux). De même, des points DE 3 et DE 4 sera symétrique par rapport à une droite UN B, si R 3 = R 4 et R 7 = R 8 .

MAIS.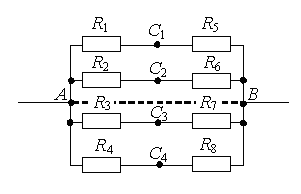

b.
Riz. une.

2 voies. Les points ont le même potentiel si les rapports de résistance entre les points donnés et les points de connexion sont égaux.

Par exemple, des points DE 1 et DE 2 (fig. 1 a) ont même potentiel, si . De même, des points DE 3 et DE 4 ont même potentiel, si .

Nous montrerons avec des exemples comment ces méthodes peuvent être utilisées pour convertir des circuits électriques.

La méthode de combinaison des nœuds équipotentiels: pointe avec les mêmes potentiels peut être connecté en nœuds .

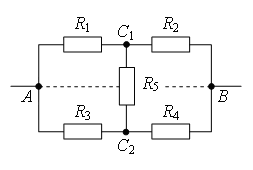
Exemple 1. Déterminer la résistance du circuit électrique (Fig. 2), si : a) R 1 = R 3 = 2R, R 2 = R 4 = R, R 5 = 3R; b) R 1 = R 4 = 2R, R 2 = 4R, R 3 = R, R 5 = 5R.

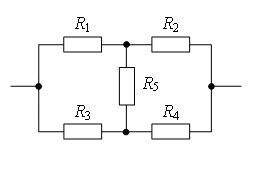
Riz. 2.

a) Si vous tracez une ligne droite à travers les points de connexion UN B(Fig. 3 a), alors les résistances des sections sont égales UA 1 et UA 2 (R 1 = R 3), et sont égaux à la résistance des sections Soleil 1 et Soleil 2 (R 2 = R 4). Par conséquent, les pointes DE 1 et DE UN B et ont le même potentiel.

Des points avec les mêmes potentiels peuvent être connectés en nœuds (Fig. 3, b). Résistances R 1 et R R 2 et R 4 - en parallèle, tronçons 1/3 et 2/4

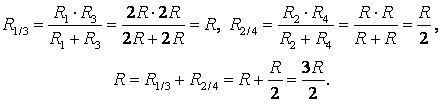
b) Si vous tracez une ligne droite UN B(Fig. 3 a), puis la résistance des sections UA 1 et UA 2 ne sont pas égaux, d'où les points DE 1 et DE 2 ne sont pas symétriques par rapport à une droite UN B. MAIS points DE 1 et DE 2 ont le même potentiel, car .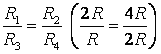

Des points avec les mêmes potentiels peuvent être connectés en nœuds (Fig. 3b). Résistances R 1 et R 3 sont connectés en parallèle et les résistances R 2 et R 4 - en parallèle, tronçons 1/3 et 2/4 séquentiellement. Par conséquent,

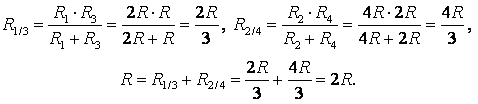
un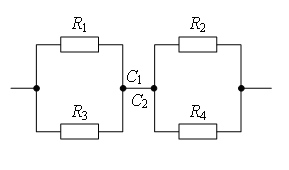

b
Riz. 3.

Exemple 2 MAIS 1 et À 3 (fig. 4). Résistance de chaque nervure R 0 .

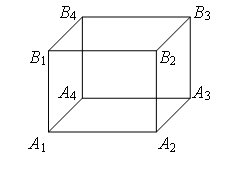
Riz. quatre.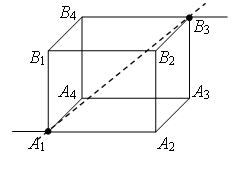

Riz. 5.

MAIS 1 À 3 (fig. 5). Les résistances sont égales (les longueurs sont égales - les nervures) des profilés MAIS 1 À 1 , MAIS 1 MAIS 2 et MAIS 1 MAIS 4 , et résistances égales (longueurs égales - diagonales) des sections À 3 À 1 , À 3 MAIS 2 et À 3 MAIS quatre. D'où les points À 1 , MAIS 2 et MAIS MAIS 1 À 3 et ont des potentiels égaux. Sont égaux à la résistance des plots MAIS 1 MAIS 3 , MAIS 1 À 2 et MAIS 1 À À 3 MAIS 3 , À 3 À 2 et À 3 À quatre. D'où les points MAIS 3 , À 2 et À 4 sont symétriques par rapport à une droite MAIS 1 À 3 et ont des potentiels égaux.

Des points avec les mêmes potentiels peuvent être connectés en nœuds (Fig. 6). Trois résistances R 0 connecté en parallèle entre les points MAIS 1 et MAIS 2 (À 1 , MAIS 4), six résistances R MAIS 2 (À 1 , MAIS 4) et MAIS 3 (À 2 , À 4), trois résistances R 0 - parallèle entre les points MAIS 3 (À 2 , À 4) et À 3, les tronçons entre ces points sont connectés en série. Par conséquent,

.



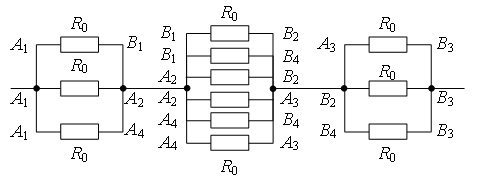
Riz. 6.

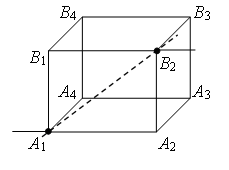
Exemple 3. Trouver la résistance du cube de fil entre les points MAIS 1 et À 2 (fig. 4). Résistance de chaque nervure R 0 .

Traçons une ligne droite à travers les points de connexion MAIS 1 À 2 (fig. 7a). Les résistances sont égales (les longueurs sont égales - les nervures) des profilés MAIS 1 À 1 , MAIS 1 MAIS 2 , et sections de résistances égales (longueurs égales - nervures) À 2 À 1 , À 2 MAIS 2. D'où les points À 1 et MAIS 2 sont symétriques par rapport à une droite MAIS 1 À 2 et ont des potentiels égaux. Sont égaux à la résistance des plots MAIS 1 MAIS 3 et MAIS 1 À 4 , et sont égaux à la résistance des plots À 2 MAIS 3 et À 2 À quatre. Par conséquent, les pointes MAIS 3 et À 4 MAIS 1 symétrique par rapport à une droite À 2 et ont des potentiels égaux.

Des points avec les mêmes potentiels peuvent être connectés en nœuds (Fig. 7 b). En utilisant la méthode récurrente, le circuit peut être simplifié (Fig. 7 c ou d).

points MAIS 2 et À 4 ont le même potentiel, car 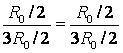. Des points avec les mêmes potentiels peuvent être connectés en nœuds (Fig. 7e). Résistances sur site MAIS 1 MAIS 2 sont connectés en parallèle, et les résistances de la section MAIS 2 À 2 - en parallèle, et ces sections sont connectées en série. Par conséquent,

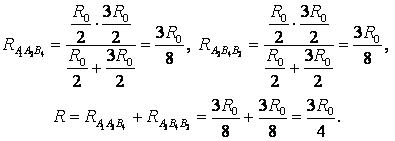
un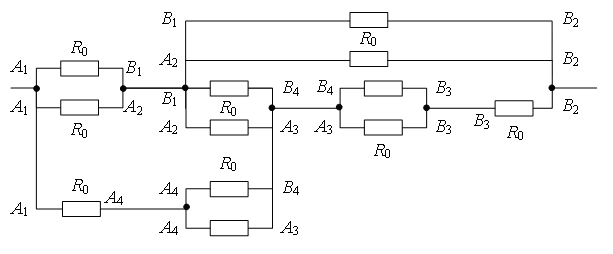



b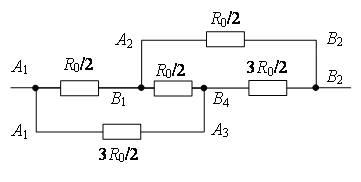

dans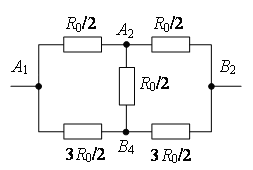

g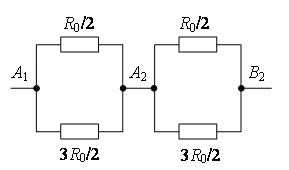

ré
Riz. sept.

S'il est possible de combiner deux nœuds équipotentiels, alors la transition inverse est également possible.

Méthode de séparation des nœuds: un nœud de circuit peut être divisé en deux ou plusieurs nœuds si les nœuds résultants ont les mêmes potentiels.

Une condition préalable pour cela est de vérifier les nœuds obtenus lors de la séparation pour l'égalité des potentiels (symétrie ou proportionnalité des résistances).

Exemple 4 Trouvez la résistance du circuit, qui est un cadre de morceaux de fil identiques (Fig. 8) avec une résistance R 0 chacun.

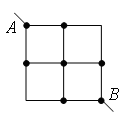
Riz. huit.

Diviser le nœud au milieu du cadre en deux nœuds O 1 et O 2 comme le montre la Fig. 9h du matin Cela peut être fait parce que les points O 1 et O 2 ont des potentiels égaux : tracés de résistance égale AO 1 , AO 2 , et sont égaux à la résistance des sections BO 1 , BO 2. Redessinons le schéma sous une forme standard (Fig. 9 b). En utilisant la méthode récurrente, le circuit peut être simplifié (Fig. 9c), car résistance de section C 1 F 1 est égal 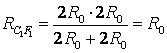, De même . Alors la résistance totale du circuit est .

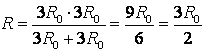Introduction

La résolution de problèmes fait partie intégrante de l'enseignement de la physique, car dans le processus de résolution de problèmes, la formation et l'enrichissement des concepts physiques ont lieu, la pensée physique des élèves se développe et leurs compétences d'application des connaissances dans la pratique s'améliorent.

Au cours de la résolution de problèmes, les objectifs didactiques suivants peuvent être définis et mis en œuvre avec succès :

• Proposer un problème et créer une situation problématique ;
• Résumer les nouvelles informations ;
• Formation de compétences et d'aptitudes pratiques;
• Vérifier la profondeur et la force des connaissances;
• Consolidation, généralisation et répétition du matériel;
• Mise en œuvre du principe des polytechniques ;
• Développement des capacités créatives des élèves.

Parallèlement à cela, lors de la résolution de problèmes, les écoliers acquièrent de l'assiduité, de la curiosité d'esprit, de l'ingéniosité, de l'indépendance dans les jugements, de l'intérêt pour l'apprentissage, de la volonté et du caractère, de la persévérance dans la réalisation de l'objectif. Pour atteindre ces objectifs, il est particulièrement pratique d'utiliser des tâches non traditionnelles.

§une. Tâches de calcul des circuits électriques CC

Selon le programme scolaire, très peu de temps est alloué à l'examen de ce sujet, de sorte que les élèves maîtrisent plus ou moins bien les méthodes de résolution de problèmes de ce type. Mais souvent ces types de tâches se retrouvent dans les tâches Olympiade, mais elles sont basées sur le cursus scolaire.

Ces tâches non standard pour le calcul des circuits électriques à courant continu comprennent des tâches dont les schémas:

2) symétrique ;

3) consistent en des composés mixtes complexes d'éléments.

En général, tout circuit peut être calculé en utilisant les lois de Kirchhoff. Cependant, ces lois ne sont pas incluses dans le programme scolaire. De plus, peu d'élèves peuvent résoudre correctement un système d'un grand nombre d'équations avec de nombreuses inconnues, et ce n'est pas la meilleure façon de perdre du temps. Par conséquent, vous devez pouvoir utiliser des méthodes permettant de trouver rapidement la résistance et la capacité des circuits.

§2. Méthode du circuit équivalent

La méthode des circuits équivalents est que le circuit d'origine doit se présenter sous forme de tronçons série, sur chacun desquels les éléments du circuit sont connectés soit en série, soit en parallèle. Pour une telle représentation, le schéma doit être simplifié. Sous la simplification du circuit, nous entendons la connexion ou la déconnexion de tout nœud du circuit, la suppression ou l'ajout de résistances, de condensateurs, en veillant à ce que le nouveau circuit d'éléments connectés en série et en parallèle soit équivalent à celui d'origine.

Un circuit équivalent est un circuit tel que lorsque la même tension est appliquée aux circuits d'origine et convertis, le courant dans les deux circuits sera le même dans les sections correspondantes. Dans ce cas, tous les calculs sont effectués avec le schéma converti.

Plusieurs astuces peuvent être utilisées pour dessiner un circuit équivalent pour un circuit avec une connexion de résistance mixte complexe. Nous nous limiterons à n'en considérer en détail qu'un seul - la méthode des nœuds équipotentiels.

Cette méthode réside dans le fait que des points de potentiels égaux se trouvent dans des circuits symétriques. Ces nœuds sont connectés les uns aux autres, et si une section du circuit était incluse entre ces points, elle est alors rejetée, car en raison de l'égalité des potentiels aux extrémités, le courant ne le traverse pas et cette section n'affecte pas la résistance totale du circuit.

Ainsi, le remplacement de plusieurs nœuds de potentiels égaux conduit à un circuit équivalent plus simple. Mais parfois, il est plus opportun de remplacer à l'envers un nœud

plusieurs nœuds avec des potentiels égaux, ce qui ne viole pas les conditions électriques dans le reste.

Considérons des exemples de résolution de problèmes par ces méthodes.

Du fait de la symétrie des branches de la chaîne, les points C et D sont équipotentiels. Par conséquent, nous pouvons exclure la résistance entre eux. Nous connectons les points équipotentiels C et D en un nœud. On obtient un circuit équivalent très simple :

dont la résistance vaut :

RAB=Rac+Rcd=r*r/r*r+r*r/r+r=r.

Tâche n° 2

Aux points F et F', les potentiels sont égaux, ce qui signifie que la résistance entre eux peut être écartée. Le circuit équivalent ressemble à ceci :

Résistances de section DNB;F`C`D`; D', N', B' ; FCD sont égaux entre eux et égaux à R1 :

1/R1=1/2r+1/r=3/2r

Dans cette optique, un nouveau circuit équivalent est obtenu :

Sa résistance et la résistance du circuit d'origine RAB est égale à :

1/RAB=1/r+R1+R1+1/r+R1+R1=6/7r

Tâche n° 3.

Les points C et D ont des potentiels égaux. L'exception est la résistance entre eux. On obtient le circuit équivalent :

La résistance RAB souhaitée est égale à :

1/RAB=1/2r+1/2r+1/r=2/r

Tâche n° 4.

Comme on peut le voir sur le schéma, les nœuds 1, 2, 3 ont des potentiels égaux. Connectons-les au nœud 1. Les nœuds 4, 5, 6 ont également des potentiels égaux - connectons-les au nœud 2. Nous obtenons le circuit équivalent suivant :

La résistance dans la section A-1, R 1 est égale à la résistance dans la section 2-B, R3 et est égale à :

La résistance dans la section 1-2 est : R2=r/6.

On obtient alors le circuit équivalent :

La résistance totale RAB est :

RAB \u003d R1 + R2 + R3 \u003d (5/6) * r.

Tâche n° 5.

Points C et F-équivalent. Connectons-les en un seul nœud. Ensuite, le circuit équivalent ressemblera à ceci :

Résistance de la section CA :

Résistance dans la section FN :

Résistance dans la section DB :

Il s'avère que le circuit équivalent:

La résistance totale souhaitée est égale à :

Tâche #6

Remplaçons le noeud commun O par trois noeuds de potentiels égaux O, O 1 , O 2 . On obtient le système équivalent :

Résistance dans la section ABCD :

Résistance dans la section A`B`C`D` :

Résistance dans la section ACB

On obtient le circuit équivalent :

La résistance totale souhaitée du circuit R AB est :

RA AB = (8/10)*r.

Tâche numéro 7.

« Divisons » le nœud O en deux angles équipotentiels O 1 et O 2 . Maintenant, le circuit peut être représenté comme une connexion parallèle de deux circuits identiques. Par conséquent, il suffit d'en considérer l'un en détail:

La résistance de ce circuit R 1 est :

Alors la résistance de tout le circuit sera égale à :

Tâche n° 8

Les nœuds 1 et 2 sont équipotentiels, alors connectons-les en un nœud I. Les nœuds 3 et 4 sont également équipotentiels - connectés à un autre nœud II. Le circuit équivalent ressemble à :

La résistance dans la section A-I est égale à la résistance dans la section B-II et est égale à :

La résistance de la section I-5-6-II est :

La résistance de la section I-II est égale à :

On obtient le circuit équivalent final :

La résistance totale du circuit souhaitée R AB \u003d (7/12) * r.

Tâche n° 9

Dans la branche OS, nous remplaçons la résistance par deux résistances connectées en parallèle de 2r chacune. Maintenant le nœud C peut être divisé en 2 nœuds équipotentiels C 1 et C 2. Le circuit équivalent dans ce cas ressemble à ceci:

Les résistances dans les sections OS I B et DC II B sont identiques et égales, car il est facile de calculer 2r. Nous dessinons à nouveau le circuit équivalent correspondant :

La résistance dans la section AOB est égale à la résistance dans la section ADB et est égale à (7/4)*r. Ainsi, on obtient le circuit équivalent final de trois résistances connectées en parallèle :

Sa résistance totale est R AB = (7/15)*r

Tâche n° 10

Les points COD ont des potentiels égaux - connectons-les en un seul nœud O je.Le circuit équivalent est représenté sur la figure :

Résistance dans la section A O jeéquivaut à . Sur le tronçon O je La résistance est égale à On obtient un circuit équivalent très simple :

La résistance ITS est égale à la résistance totale souhaitée

Les problèmes n° 11 et n° 12 sont résolus d'une manière légèrement différente des précédents. Dans le problème 11, une propriété spéciale des chaînes infinies est utilisée pour le résoudre, et dans le problème 12, une méthode de simplification de chaîne est utilisée.

Tâche numéro 11

Distinguons un maillon se répétant à l'infini dans cette chaîne ; dans ce cas, il s'agit des trois premières résistances. Si nous éliminons ce lien, la résistance totale du circuit infini R ne changera pas, car exactement le même circuit infini se révélera. De plus, rien ne changera si nous reconnectons le lien sélectionné à la résistance infinie R, mais il convient de noter qu'une partie du lien et le circuit infini avec la résistance R sont connectés en parallèle. On obtient ainsi le circuit équivalent :

Il s'avère que les équations

En résolvant le système de ces équations, on obtient :

§3. Apprendre à résoudre des problèmes de calcul de circuits électriques par la méthode des nœuds équipotentiels

Une tâche est un problème pour lequel l'élève aura besoin de raisonnement logique et d'inférence. Construit sur la base des lois et des méthodes de la physique. Ainsi, à l'aide de tâches, la pensée délibérée des élèves est activée.

Dans le même temps. Les connaissances théoriques ne peuvent être considérées comme acquises que lorsqu'elles sont appliquées avec succès dans la pratique. Les problèmes de physique décrivent des problèmes souvent rencontrés dans la vie et au travail, qui peuvent être résolus en utilisant les lois de la physique, et si l'étudiant résout avec succès les problèmes, alors on peut dire qu'il connaît bien la physique.

Pour que les élèves réussissent à résoudre des problèmes, il ne suffit pas de disposer d'un ensemble de méthodes et de méthodes de résolution de problèmes, il est également nécessaire d'enseigner spécifiquement aux écoliers comment utiliser ces méthodes.

Considérons un plan pour résoudre les problèmes de calcul des circuits électriques à courant continu par la méthode des nœuds équipotentiels.

1. Condition de lecture.
2. Brève déclaration de l'état.
3. Convertir en unités SI.
4. Analyse des circuits :
1. déterminer si le circuit est symétrique ;
2. établir des points d'égalité de potentiel ;
3. choisissez ce qu'il est plus opportun de faire - connectez des points de potentiels égaux ou, au contraire, divisez un point en plusieurs points de potentiels égaux;
4. tracer un circuit équivalent ;
5. trouver des sections avec uniquement une connexion en série ou uniquement en parallèle et calculer la résistance totale dans chaque section selon les lois de la connexion en série et en parallèle ;
6. dessiner un circuit équivalent, en remplaçant les sections par leurs résistances de conception correspondantes ;
7. répétez les étapes 5 et 6 jusqu'à ce qu'il reste une résistance dont la valeur sera la solution au problème.
5. Analyse de la réalité de la réponse.

En savoir plus sur l'analyse de schéma

a) déterminer si le circuit est symétrique.

Définition. Un circuit est symétrique si une moitié est une image miroir de l'autre. De plus, la symétrie ne doit pas seulement être géométrique, mais les valeurs numériques des résistances ou des condensateurs doivent également être symétriques.

Le circuit est symétrique puisque les branches ASV et ADV sont géométriquement symétriques et que le rapport de résistance dans une section AS:AD=1:1 est le même que dans l'autre section SD:DV=1:1.

Le circuit est symétrique, car le rapport des résistances dans la section AC:BP=1:1 est le même que dans l'autre section SV:DV=3:3=1:1

Le circuit n'est pas symétrique, puisque les rapports des résistances sont numériquement

non symétrique -1:2 et 1:1.

b) établir des points de potentiels égaux.

À partir de considérations de symétrie, nous concluons que les potentiels sont égaux aux points symétriques. Dans ce cas, les points symétriques sont les points C et D. Ainsi, les points C et D sont des points équipotentiels.

c) choisir ce qu'il est opportun de faire - connecter des points de potentiels égaux ou, inversement, diviser un point en plusieurs points de potentiels égaux.

Nous voyons dans cet exemple qu'une résistance est incluse entre les points de potentiels égaux C et D, à travers lesquels aucun courant ne circulera. Par conséquent, nous pouvons éliminer cette résistance et connecter les points C et D en un seul nœud.

d) tracer un circuit équivalent.

Nous dessinons un circuit équivalent. Dans ce cas, on obtient un schéma avec les points C et D connectés en un point.

e) trouver des sections avec uniquement une connexion en série ou uniquement en parallèle et calculer la résistance totale dans chacune de ces sections selon les lois de la connexion en série et en parallèle.

D'après le circuit équivalent résultant, on peut voir que dans la section AC, nous avons deux résistances connectées en parallèle. Leur résistance totale se trouve selon la loi de mise en parallèle :

1/ Rtot=1/R1+1/R2+1/R3+…

Ainsi 1/RAC=1/r+1/r=2/r, d'où RAC= r/2.

Sur la section NE, l'image est similaire :

1/RCB= 1/r+1/r =2/r, d'où RCB=r/2.

e) dessiner un circuit équivalent, en remplaçant les sections par leurs résistances de conception correspondantes.

Nous dessinons un circuit équivalent en y substituant les résistances calculées des sections RAC et RCB :

g) points e) et f) répéter jusqu'à ce qu'il reste une résistance dont la valeur sera la solution du problème.

Nous répétons le paragraphe e): sur la section AB, nous avons deux résistances connectées en série. Leur résistance totale se trouve selon la loi de connexion en série :

Rtot= R1+R2+R3+… soit RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Nous répétons le paragraphe e): tracer un circuit équivalent :

Nous avons obtenu un circuit avec une résistance dont la valeur est égale à la résistance du circuit d'origine. Ainsi, nous avons obtenu la réponse RAB = r.

Littérature

1. Balash. VIRGINIE. problèmes de physique et méthodes pour les résoudre. - M : Lumières, 1983.
2. Lukashik V.I. Olympiade de Physique - M: Education, 2007
3. Usova A.V., Bobrov A.A. Formation des compétences pédagogiques et des capacités des étudiants en cours de physique - M: Education, 1988
4. Khatset A. Méthodes de calcul pour les circuits équivalents // Kvant.
5. Chertov A. G. Livre de tâches en physique. - M. : Ecole Supérieure, 1983
6. Ziyatdinov Sh.G., Solovyanyuk S.G. (directives) Birsk, 1994
7. Maron A.E., Maron E.A. La physique. Matériel didactique. Moscou, "Drofa", 2004